1.      Įvadas. Bendrosios žinios.

Ekonometrika nagrinėja ekonominių procesų statistinių modelių sudarymo bei jų modeliavimo problemas. Tai viena iš bazinių ekonominio lavinimo disciplinų. Klasikinėje ekonometrikos teorijoje nagrinėjamos trys pagrindinės problemos: regresijos modelių sudarymas, laiko eilučių prognozavimas, ekonometrinių lygčių sistemų tyrimas. Pagrindinis ekonometrikos tikslas – ekonometrikos modelio sudarymas. Modelis yra sudėtingos tikrovės ir abstrakčios mokslinės teorijos tarpinė grandis. Modeliu vadiname realaus objekto dirbtinį ar realų atvaizdą, leidžiantį nagrinėti tam tikras originalo savybes. Modelio sudarymas – tai daug darbo reikalaujantis, sudėtingas procesas.

Pagal atsitiktinumo nustatymo pobūdį modeliai gali būti determinuoti arba stochastiniai.

Determinuotuose modeliuose visi kintamieji, nusakantys modelio funkcionavimą, laikomi determinuotais, t.y. įgyjančiais tam tikras fiksuotąsias reikšmes. Jei modelio kintamieji yra tikimybinės kilmės ir juos nusako atsitiktiniai dydžiai, tai stochastiniai modeliai.

Atsižvelgiant į laiko veiksnį, kuriuo aspektu nagrinėjamas objektas, visi modeliai skirstomi į statinius ir dinaminius. Didžioji dauguma praktiškai sprendžiamų uždavinių yra statiniai. Šiuose modeliuose tiek priklausomi, tiek nepriklausomi kintamieji yra fiksuoti tam tikram laiko tarpui. Dinaminiuose modeliuose kintamieji kinta laike.

Ekonometrika yra mokslas, kuris tiria kiekybinius ekonominių procesų dėsningumus bei kintamųjų tarpusavio priklausomybes, siekiant prognozuoti šių procesų vystymąsi. Pagrindinis uždavinys – ekonominio modelio sudarymas ir jo galimų panaudojimo sričių, aprašant, analizuojant ir prognozuojant realius ekonominius procesus, nustatymas.

Ekonomikos teorijoje formuluojami teiginiai arba hipotezės, kurios dažniausiai iš prigimties yra kokybinės. Pavyzdžiui, mikroekonomikos teorija teigia, jog sumažinus prekės kainą, galima tikėtis, kad padidės šios prekės paklausa. Taigi, ekonomikos teorija postuluoja neigiamą, arba atvirkštinį, kainos ir parduodamo prekės kiekio ryšį. Tai yra žinoma kaip paklausos dėsnis. Bet pati teorija nepateikia jokio skaitmeninio matavimo metodo šio ryšio stiprumui nustatyti. Praktiškai nėra įmanoma pasakyti, kaip pasikeis pardavimų apimtis, pakitus prekės kainai. Tad ekonometrikos paskirtis kaip tik yra pateikti reikiamą skaitmeninį įvertinimą. Kitaip tariant, ekonometrika nurodo daugumos ekonomikos teorijos teiginių empirinę (pagrįstą stebėjimais) arba eksperimentinę priklausomybę.

Matematinės ekonomikos pagrindinis interesas – ekonomikos teoriją išreikšti matematine forma (modeliu), nereikalaujant empiriškai patikrinti teorijos.

Tirdamas paklausos dėsnį, matematikas gali pasiūlyti  šio dėsnio tiesinį, hiperbolinį ar kitą modelį. Faktiškai matematikas pasiūlo priklausomybės funkcijos tipą, tačiau lieka neaiškios šios funkcijos parametrų konkrečios reikšmės. Ekonometrikas kaip tik ir pasirenka vieną iš siūlomų priklausomybės tipų, jo nuomone, geriausiai tinkantį realiam procesui aprašyti.

Svarbiausias ekonometriko uždavinys – sudaryti ekonometrikos modelį. Sudarant modelį, svarbu žinoti, kad tai yra supaprastintas realaus proceso atvaizdas. Pavyzdžiui, pasakymas, kad medvilninio audinio paklausa priklauso nuo jo kainos, yra supaprastintas, nes visi supranta, kad yra aibė kitų kintamųjų, kurie gali lemti medvilninio audinio kainą: viskozės audinio kaina, mados tendencijos, metų laikas, kuro kainų augimas ir pan.

Praktiškai į modelį įtraukiami tie kintamieji, kurie laikomi naudingais siekiamiems tikslams, o visi kiti priskiriami aibei, vadinamai „triukšmu“. Pastarųjų kintamųjų egzistavimas leidžia suformuluoti teiginį, kad visuomet esama stebėjimo paklaidų, ir jos pasiskirsčiusios pagal tam tikrus skirstinius. Ekonometrikos modeliuose daroma prielaida, kad šis triukšmas yra „baltasis triukšmas“, o jam būdinga tai, kad šios paklaidos skirtingais laiko momentais yra nepriklausomos ir pasiskirsčiusios pagal normalųjį skirstinį su vidurkiu, lygiu 0, ir dispersija σ².

Svarbi ekonometrikos sąvoka – atsitiktinis dydis. Tai dydis, turintis fizinę prasmę, išmatuojamas, o jo reikšmė nustatoma konkretaus stebėjimo metu. Atsitiktinio dydžio sąvoka atsižvelgia į tai, kad esama nemažai žinomų arba nežinomų tikimybinių skirstinių galimai šio dydžio reikšmių aibei.

Atsitiktinio dydžio pavyzdžiu gali būti dydis – „laikas sugaištamas pietums“. Kiekvienu konkrečiu atveju šio laikotarpio trukmė priklauso nuo norimų patiekalų, žmonių skaičiaus valgykloje, apmokėjimo būdo, valandos, kada pietaujama ir pan. Visiškai tiksliai apskaičiuoti šios trukmės reikšmės neįmanoma, nes ją veikia daug tiksliai neįvertinamų išorinių veiksnių. Tačiau atsitiktiniam dydžiui būdinga tai, kad, daug kartų įvykiui kartojantis, galima nustatyti tikėtiną vidutinę įvykio reikšmę.

Atskirai pažymėtinas sąvokų atsitiktinis dydis ir atsitiktinis kintamasis santykis. Atsitiktinis kintamasis yra atsitiktinis dydis, kuris įvertinamas tiriamajame ekonominiame procese atsižvelgiant į šio proceso vidinę struktūrą. Faktiškai tai yra iš visos galimos atsitiktinių dydžių aibės atrinktas dydis, kuris nusako tam tikras ekonominio proceso savybes. Atsitiktiniam kintamajam galioja visos atsitiktinių dydžių savybės. Tad ekonometrikoje vietoj atsitiktinio dydžio sąvokos bus vartojama atsitiktinio kintamojo sąvoka.

Ekonometrikoje svarbus dėmesys tenka laiko eilutėms. Laiko eilutė – tai rinkinys atsitiktinio kintamojo X reikšmių, gautų tam tikrais fiksuotais laiko momentais.

Kai duomenys renkami reguliariais laiko intervalais (pvz. kas savaitę), reikšmę įgyja ne tik patys duomenys, bet ir jų gavimo tvarka. Tiriant laiko eilutes, laikoma, kad yra žinomos reikšmės x(t_i), i=1,…,n laiko momentais t₁<t₂<...<t_n ir visi stebėjimai atliekami vienodais laiko intervalais, t.y. t_i+1-t_i=Δt. Visi šie surinkti duomenys sudaro stebinių aibę.

Kai stebime vieno ekonominio kintamojo reikšmių kaitą, gauname vienmatę laiko eilutę. Kai stebime vieno objekto k ekonominių kintamųjų reikšmių kaitą, gauname daugiamatę laiko eilutę.

Jei laikas yra nenutrūkstamas, tai laiko eilutė vadinama tolydine; ji žymima X(t), pvz. elektrokardiograma. Jei laikas yra diskretinis, tai laiko eilutė vadinama diskretine; ji žymima X_t. Tiriant ekonominius procesus, dažniausiai analizuojamos diskretinės laiko eilutės.

Laiko eilutės gali būti momentinės (pirkėjų skaičius parduotuvėje) ir intervalinės (per mėnesį realizuotos produkcijos apimtys). Ekonominiuose tyrimuose svarbesnės intervalinės laiko eilutės.

Analizuojant laiko eilutes, visuomet tiriama viena atsitiktinio proceso realizacija. Atsitiktinis arba stochastinis procesas yra atsitiktinio kintamojo reikšmių, užfiksuotų laike, rinkinys. Ekonominių procesų laiko eilutė užrašoma x₁,…,x_t,…,x_n, kurioje x_t nurodo atsitiktinio kintamojo X reikšmę t–uoju laikotarpiu.  Skirtumas tarp atsitiktinio proceso ir jo realizacijos yra panašus kaip ir skirtumas tarp populiacijos ir imties. Kaip pagal imties duomenis daromos prielaidos apie populiacijos savybes, taip ir laiko eilutėse, turint realizacijos duomenis, daromos prielaidos apie atsitiktinį procesą.

Kiekvieną laiko eilutės momentinę reikšmę lemia daugybė veiksnių, kuriuos galima suskirstyti į tris grupes:

1.             veiksniai, formuojantys vidurkio funkcijos kitimą;

2.             veiksniai, formuojantys sezoninius svyravimus;

3.             atsitiktiniai veiksniai, formuojantys stacionarų procesą su nuliniu vidurkiu.

 

Ekonometrikoje naudojamas laiko eilučių modelis gali būti užrašomas dvejopai: adityviuoju modeliu arba multiplikatyviuoju. Adityvusis atrodo šitaip:

,(1.1)

kur m_t – vidurkio funkcija, s_t – sezoniškumo dedamoji, u_t – triukšmo dedamoji, t.y. stacionarus nulinio vidurkio atsitiktinis procesas.

Multiplikatyvusis laiko eilutės modelis yra:

.(1.2)

Vidurkio funkcijos pavidalas priklauso nuo laiko eilutės stacionarumo. Stacionariame procese laiko eilutės reikšmės kinta atsitiktinai kiekvienu momentu, tačiau vidurkis gana ilgą laiką nekinta, t.y. m_t= m.

Nestacionarių laiko eilučių vidurkis nėra pastovus, bet ilgainiui kinta. Kintamas laiko eilutės vidurkis vadinamas trendu. Pagal pobūdį trendai skirstomi į tiesinius ir netiesinius. Jei tiriamosios laiko eilutės trendo funkcija skiriasi nuo tiesinės, galima atlikti duomenų transformaciją tiesiškumo pagerinimui.

Esant sezoniniam trendui, vidurkis kinta cikliškai tam tikrais laiko periodais. Sakoma, kad laiko eilutė yra ciklinė, jei jos savybės kartojasi po L laiko intervalų (metai, ketvirčiai, mėnesiai ir t.t.). Skaičius L vadinamas ciklo periodu.

Cikliškumu pasižymintiems ekonominiams procesams, vartojama sezoniškumo sąvoka. Sezoniškų ekonominių procesų laiko eilučių pavyzdžiai: poilsiautojų skaičius Druskininkuose, suvalgomų ledų kiekis, oro temperatūra Lietuvoje. Sezoninį trendą nusako sezoniškumo koeficientai; jie lygūs einamajai rodiklio reikšmei, padalytai iš ciklo vidutinės rodiklio reikšmės.

Pažymėtina, kad stacionarumo identifikavimas yra vienas iš pagrindinių laiko eilučių modeliavimo uždavinių.

Ekonometrikoje naudojama laginio kintamojo sąvoka, kuri gali būti panaudota tiek ir nepriklausomam, tiek ir priklausomam kintamajam. Laginis kintamasis tai kintamasis, kurio reikšmės išmatuotos prieš tai buvusiuose laikotarpiuose. Jei Y_t yra priklausomas kintamasis, tai Y_t-1,…, Y_t-l yra šio kintamojo laginiai kintamieji.

Ekonometrikos modelio formalus aprašas pateikiamas matematinės lygties arba lygčių sistemos pavidalu. Užrašant modelį viena lygtimi, priklausomai nuo to, kokie kintamieji įtraukiami į modelio lygtį, galimos šios ekonometrikos modelių užrašymo formos:

1.             klasikinės regresijos modelis,

2.             netiesinės regresijos modelis,

3.             redukuotos formos modelis.

Klasikiniame regresijos modelyje kiekvienam endogeniniam kintamajam užrašoma tiesinė vien tik egzogeninių kintamųjų funkcija. Bendruoju atveju ši modelio lygtis užrašoma pavidalu

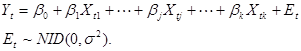(1.3)

NID užrašas parodo, kad tai yra normalusis nepriklausomai pasiskirstęs dydis su nuliniu vidurkiu ir dispersija σ².

Redukuotos formos modelyje kiekvienam endogeniniam kintamajam užrašytoje lygtyje įeina ir egzogeniniai kintamieji, ir laginiai endogeniniai kintamieji. Klasikinis regresijos modelis yra dalinis atvejis redukuotos formos modelio, į kurį įeina tik egzogeniniai kintamieji. Šio modelio formos (redukuotos formos) vienas iš paprasčiausių lygties užrašymo pavidalų būtų

(1.4)

Šie modeliai dažnai naudojami, modeliuojant laiko eilutes.

Tiriant ekonominius procesus dažnai nepakanka vienos lygties modelio, nes reikia aprašyti priklausomybes, kurios įvertina egzistuojančią tarp kintamųjų struktūrą.

Lygčių sistemos ekonometriniuose tyrimuose gali būti sudaromos dvejopai: nepriklausomų lygčių sistema, ekonometrinių lygčių sistema.

Nepriklausomų lygčių sistemoje kiekvienas endogeninis kintamasis Y nagrinėjamas kaip funkcija to paties egzogeninių kintamųjų X={x₁,x₂,...,x_k} rinkinio.

Ekonometrinių lygčių sistema vadinama tarpusavyje susietų regresijos modelių visuma, kurioje tie patys kintamieji vienose lygtyse gali būti vertinami kaip egzogeniniai kintamieji, o kitose – kaip endogeniniai kintamieji.

Ekonometrinių lygčių sistemos užrašymo forma vadinama struktūrine modelio forma ir tokia užrašymo forma fiksuoja tik pačią ekonominės sistemos struktūrą. Struktūriniuose modeliuose dešinėje lygties pusėje be egzogeninių kintamųjų yra naudojami ir endogeniniai laginiai kintamieji.

Ekonometrinių lygčių sistema užrašoma

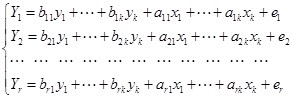(1.5)

Dešinėje lygties pusėje užrašomi koeficientai b_j prie endogeninių kintamųjų ir koeficientai a_j prie egzogeninių kintamųjų. Šie koeficientai vadinami modelio struktūriniais koeficientais. Dažniausiai šio modelio kintamieji yra normalizuojami, t.y. jie užrašomi kaip nuokrypiai nuo vidurkių ir todėl šio modelio lygtyse neegzistuoja laisvojo nario.

Sudarant ekonometrinius modelius yra išskiriami 6 etapai:

1.             preliminari tiriamo ekonominio proceso analizė,

2.             stebinių surinkimo plano sudarymas,

3.             stebinių surinkimas ir įvedimas į kompiuterį,

4.             preliminari stebinių analizė (pradinis stebinių apdorojimas),

5.             įvertinimo procedūrų parinkimas ir realizavimas,

6.             ekonominio tyrimo rezultatų apibendrinimas.

 

Ketvirtasis punktas – pradinis stebinių apdorojimas apima eilę uždavinių, tokių kaip kintamųjų kitimo intervalų numatymas; ryškiai išsiskiriančių reikšmių nustatymas; praleistų stebinių atkūrimas; duomenų statistinės nepriklausomybės patikrinimas; nagrinėjamos stebinių aibės  aprašymas eksperimentiniais skirstiniais; skirtingų pradinių duomenų grupių vienarūšiškumo patikrinimas. Pradinis stebinių apdorojimas yra labai svarbus tyrimo etapas, todėl jo punktus naudinga pakomentuoti.

Atliekant išskirčių nustatymą, kai kyla abejonių dėl informacijos teisingumo, reikia atsakyti į klausimą, ar šiuos pastebėtus nukrypimus sąlygojo atsitiktinis kintamojo kitimas, ar standartinių duomenų surinkimo sąlygų pasikeitimas, ar tai yra tiesioginės klaidos. Paskutiniais dviem atvejais šiuos duomenis iš stebinių matricos reikia išbraukti. Sprendžiant išskirčių problemą, reikia patikrinti duomenų fiksavimo sąlygas. Kadangi, ne visada įmanoma tai atlikti, todėl naudojamasi statistiniu formaliu kontrolės metodu. Dažniausiai naudojamasi paprasta „trijų sigmų“ taisykle (esant normaliai pasiskirsčiusiems duomenims).

Sudarant ekonometrikos modelius, praleistos stebinių reikšmės dažniausiai pakeičiamos vidurkio reikšme.

Prieš pradedant statistinį ekonominių procesų tyrimą reikia išsiaiškinti, ar duomenys yra statistiškai nepriklausomi, ar juos reikia nagrinėti kaip tarpusavyje susijusių dydžių seką. Mat, daugumos statistinių duomenų panaudojimas paremtas hipoteze apie stebinių priklausomybę.

Dar viena svarbi pradinio stebinių apdorojimo dalis – nagrinėjamų stebinių aprašymas eksperimentiniais skirstiniais. Šiame etape apskaičiuojamos pagrindinės skaitinės charakteristikos – vidurkis, dispersija, asimetrijos ir eksceso koeficientai; o daugiamačiu atveju – kovariacinės ir koreliacinės matricos elementai. Tiriant laiko eilutes, įvertinamos autokoreliacinės funkcijos. Taip pat šiame etape atliekama skaitmeninė bei grafinė analizuojamo vienmačio kintamojo statistinė analizė, sudarant dažnių daugiakampius, histogramas, empirines skirstinio funkcijas (sukauptųjų dažnių laužtė). Šio eksperimentinio tyrimo rezultatai, kartu su apriorinėmis žiniomis apie analizuojamų objektų prigimtį, dažnai įgalina pasirinkti teisingą konkuruojančią hipotezę apie skirstinio tipą. Hipotezėms patikrinti naudojami įvairūs statistiniai kriterijai.

Taip pat svarbus skirtingų pradinių duomenų grupių vienarūšiškumo patikrinimas. Praktiškai dažnai susiklosto situacija, ypač pasyvaus eksperimento metu, kai visą stebinių matricą sudaro kelios stebinių matricos, kurios buvo fiksuotos poaibiui visų stebimų objektų. Be to, šios skirtingos pradinių duomenų imtys dar gali būti fiksuojamos skirtingais laiko momentais. Savaime suprantama, kad šioje situacijoje tyrinėtojui iškyla klausimas, ar galima šias skirtingas duomenų imtis sujungti į vieną stebinių matricą, ar  kiekvieną imtį traktuoti kaip atskirą visumą. Formuluojant šį uždavinį statistikos terminais, jis traktuojamas kaip klausimas, ar galima tvirtinti, kad šių atskirų duomenų imtys vienodos ir yra  tos pačios populiacijos atsitiktinės imtys. Ši problema dažniausiai sprendžiama analizuojant dispersinės analizės rezultatus.

Modeliuojant su ekonominiais duomenimis, dažna situacija yra tokia, kad matuojant kintamuosius skirtingais mato vienetais, sunku juos tarpusavyje palyginti. Tokiu atveju atliekama duomenų transformavimo procedūra.

Duomenų reikšmių transformavimui naudojamos šios procedūros: standartizavimas, normalizavimas, normavimas.

Standartizuotų kintamųjų reikšmės apskaičiuojamos taip:

,(1.6)

kur s_x, požymio reikšmių standartinis nuokrypis. Tokiu būdu transformavus duomenis, jų vidurkis tampa lygus 0, o dispersija 1.

Normalumo pagerinimas atliekamas tokiu būdu:

.(1.7)

Norint, kad požymio reikšmės sumažėtų taip, kad bendra jų suma būtų lygi vienam, atliekamas toks transformavimas:

.(1.8)

Norint požymio reikšmes pakeisti tokiomis, kurių minimali reikšmė būtų lygi nuliui, o maksimali – vienam, atliekamas toks normavimas, t.y. kiekviena to požymio reikšmė x_i transformuojama pagal formulę:

.(1.9)

Modeliuojant svarbus vaidmuo tenka normalumo prielaidai, todėl tenka tikrinti hipotezę apie normalųjį dėsnį. Mat, daugumai klasikinių statistikos teiginių galioja reikalavimas, kad atsitiktinis kintamasis būtų normalus arba beveik normalus. Duomenų normalumą įvertinant preliminariai naudojamos histogramos, tankio grafikai, kvantilių grafikai. Histogramos ir empirinio tankio grafikai leidžia susidaryti teisingą skirstinio formos vaizdą ir nustatyti duomenų atitiktį normalumo reikalavimui.

Norint duomenų normalumą įvertinti tiksliai, pasitelkiami Pirsono, Romanovskio bei Kolmogorovo-Smirnovo kriterijai. Pirmieji du naudoja „chi kvadratu“ skirstinį, o paskutinysis – K(λ) skirstinį.

Jei duomenys nėra pasiskirstę normaliai, galima juos priartinti prie normalaus dėsnio. Tam yra atliekamos transformacijos, tokios kaip logaritmavimo ar Box-Koks procedūra.