2.      Ekonometriniai modeliai

2.1.      Klasterizavimas

Klasterinė analizė – daugiamatis statistinis metodas, identifikuojantis egzistuojančias grupes objektų aibėje, kurioje kiekvienas objektas yra nusakomas požymių vektoriumi. Klasteris – panašių objektų grupė. Jo viduje skirtumai tarp objektų turi būti kuo mažesni, o tarp klasterių kuo didesni. Klasteriai pasižymi tuo, kad yra nebūtinai vienodo didumo, objektai į klasterį patenka pagal tam tikrus panašumus, klasterio forma priklauso nuo to, pagal kokius požymius klasterizuojama, klasteryje objektai panašesni, o tarp klasterių skirtingesni.

Svarbiausi klasterizavimo etapai yra šie:

1.             pasirenkami klasterizavimo objektai,

2.             pasirenkami požymiai, t.y. nusprendžiama pagal kokius požymius klasterizuosime,

3.             pasirenkamas objektų panašumo matas,

4.             vienu ar kitu metodu suskirstomi objektai į klasterius,

5.             peržiūrimi gauti rezultatai.

 

Objektų panašumo matai dažniausiai naudojami šie:

1.             metriniai atstumo matai,

2.             koreliacijos koeficientai,

3.             asociatyvumo koeficientai.

 

Metriniai atstumo matai gali būti vadinami skirtingumo matais, nes kuo reikšmė didesnė, tuo objektai labiau skiriasi. Šių matų yra įvairių, kur labiausiai naudojami būtų Euklido, Minkovskio, Čebyšovo, Mahalanobio atstumo kvadratas ir kt.

Pateiksime keletą metrinių atstumo matų tarp objektų X ir Y:

Euklido

(2.2)

čia m – požymių skaičius.

Euklido atstumo kvadratas

(2.3)

Manheteno

(2.4)

Čebyšovo

(2.5)

Mahalanobio atstumo kvadratas

.(2.6)

V - požymių vektorių reikšmių kovariacinė matrica, x=(x₁, x₂,...,x_m)′, y=(y₁, y₂,...,y_m)′.

Koreliacijos koeficientai – kintamųjų panašumo matai. Jei duomenys kiekybiniai, objektų panašumui įvertinti galima taikyti tiesinės koreliacijos koeficientą.

.(2.7)

Asociatyvumo koeficientai naudojami kai požymiai yra kokybiniai. Objektai yra panašesni, kuo daugiau yra sutampančių vektorių X ir Y koordinačių. Kuo didesnė koeficiento reikšmė, tuo objektai nepanašesni. Bendruoju atveju, kai matuojami kokybiniai požymiai, dažniausiai taikomas asociatyvumo koeficientas yra

,(2.8)

kur  - nesutampančių požymių reikšmių skaičius.

2.1 uždavinys.

2.1 lentelė. 2.1 uždavinio duomenys. 1 reiškia „taip“, o 0 – „ne“.

Palyginus pirmą objektą su antru ir trečiu matome, jog pirmas panašesnis su antru, nei su trečiu:

; .

Klasteriai yra sudaromi įvairiais metodais. Jie vieni nuo kitų skiriasi tuo, jog parenkami skirtingi objektų panašumo matai, naudojami skirtingi atstumų tarp klasterių nustatymo kriterijai bei skirstymo į klasterius strategija.

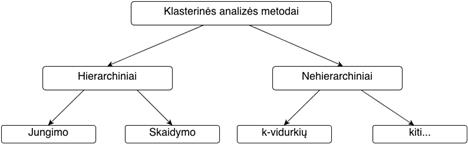
2.2 pav. Klasterinėsanalizės metodų schema

Hierarchiniai metodai. Objektai yra laikomi vienu dideliu klasteriu, kurį sudaro mažesni klasteriai, mažesnius dar mažesni ir t.t. Taikant šiuos metodus yra nustatoma klasterių tarpusavio  hierarchija (klasterių tarpusavio priklausomybių struktūra). Po to sprendžiama kiek yra klasterių (koks optimalus skaičius klasterių). Hierarchiniai metodai yra: jungimo ir skaidymo. Jungimo metodai smulkius klasterius apjungia į stambesnius, tuos stambesnius į dar stambesnius ir t.t., kol lieka vienas klasteris. Priešingybė jungimo metodui - skaidymo metodas.

2.1.1.          Hierarchinių jungimo metodų strategija.

1.             Yra N klasterių po 1 objektą ir atstumų simetrinė matrica d_ij dydžio NxN.

2.             Pagal tą atstumų matricą dij yra nustatomi du klasteriai, kurie yra panašiausi, t.y., tarp kurių atstumas yra mažiausias. Tarkim, klasteriai U ir V.

3.             Šie klasteriai, U ir V, sujungiami ir pavadinami nauju vardu (U, V).
Tada pakeičiama atstumų matrica d_ij, perskaičiuojant atstumus tarp naujo klasterio (U, V) ir kitų klasterių. Daroma taip: išbraukiame eilutes ir stulpelius, atitinkančius klasterius U ir V; pridedame eilutę ir stulpelį su atstumais tarp (U, V) ir likusiųjų klasterių.

4.             Kartojami 2) ir 3) žingsniai, kol rezultate lieka vienas klasteris.

Taikant hierarchinių jungimo metodų strategiją, yra reikalinga pasirinkti klasterių jungimo metodą.

Klasterių jungimo metodų yra įvairių. Galima jungti klasterius naudojant artimiausio, tolimiausio kaimyno panašumo matą ir kitus.

Dažniausiai naudojami panašumo matai, t.y., atstumai d(U, V), tarp dviejų klasterių U ir V yra tokie:

Artimiausio kaimyno (vienetinės jungties)

(2.9)

Tolimiausio kaimyno (pilnosios jungties)

(2.10)

Centrų

,(2.11)

kur  - klasterius sudarančių objektų požymių vektorių vidurkiai.

Vidutinės jungtie

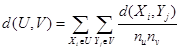,(2.12)

kur n_u – klasterio U objektų skaičius, n_v - klasterio V objektų skaičius.

Kaip jungiami klasteriai, yra pavaizduota žemiau esančiuose paveikslėliuose.

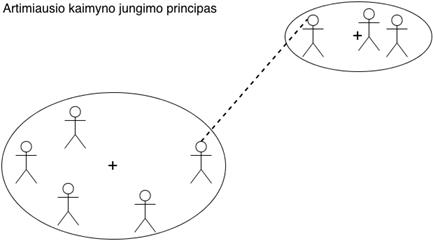
2.3 pav. Artimiausio kaimyno, klasterių jungimo principas.

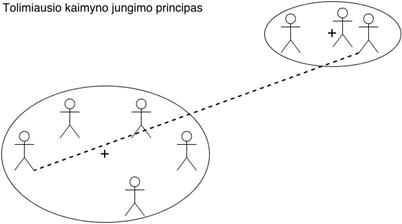
2.4 pav. Tolimiausio kaimyno, klasterių jungimo principas.

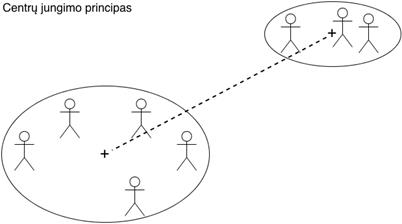
2.5 pav. Centrų, klasterių jungimo principas.

Nehierarchiniai metodai taikomi, kai žinomas klasterių skaičius arba pasirenkamas. Labai dažnai naudojamas iš jų metodas – tai k-vidurkių. Čia pasirenkamas klasterių skaičius iš anksto, tačiau klasterizavimas yra duomenų egzistuojančių struktūrų paieška, ir, iš anksto nustačius klasterių skaičių yra „primetama“ struktūra dirbtinai.

k-vidurkių metodas naudojamas, kai objektų skaičius yra didesnis už 300, nes objektų atstumų matrica tampa labai didelė. Tokiu atveju naudojami ir kiti nehierarchiniai metodai. K-vidurkių metodo esmė tokia:

1.             objektai suskirstomi į k pradinių klasterių,

2.             apskaičiuojamas kiekvieno objekto atstumas iki klasterių centrų (Euklido atstumas). Objektas skiriamas į artimiausią klasterį. Tada vėl perskaičiuojami klasterių centrai,

3.             antras žingsnis kartojamas tol, kol perskirstymų daugiau nėra.

 

2.2 uždavinys.

2.2 lentelė. 2.2 uždavinio duomenys.

Suklasterizuoti objektus hierarchinio jungimo metodu, naudojant objektų panašumo matą – Čebyšovo atstumą. Atstumas tarp klasterių turi būti skaičiuojamas tolimiausio kaimyno jungimo metodu. Taigi, pagal Čebyšovo matą

(2.13)

sudarome atstumų d_ij matricą:

2.3 lentelė. 2.2 uždavinio atstumų matrica.

Labiausiai panašūs 3 ir 2 objektai, todėl juos apjungiame į klasterį (2,3). Toliau perskaičiuojame atstumus nuo klasterio (2,3) iki kitų klasterių pagal tolimiausio kaimyno jungimo metodą:

.(2.14)

 

2.4 lentelė. 2.2 uždavinio atstumų matrica. Apjungiami 2 ir 3 objektai.

2.5 lentelė. 2.2 uždavinio atstumų matrica. Apjungiami 5 ir 1 objektai.

2.6 lentelė. 2.2 uždavinio atstumų matrica. Apjungiami 6 ir 4 objektai.

Nubrėžiame dendrogramą:

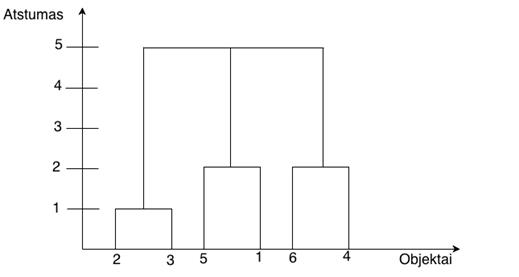
2.6 pav. 2.2 uždavinio dendrograma.

Panašiausi objektai yra antras ir trečias, nes tarp jų atstumas lygus vienam. Šeštas ir ketvirtas objektai yra tokio pat panašumo, kaip ir penktas su pirmu, nes tiek vienų, tiek kitų atstumas yra vienodas, lygus dviem.

Klasterius apibūdina įvairios charakteristikos, pavyzdžiui, forma, požymių vektorių išsibarstymas apie klasterio centrą ir kt., tačiau neturint išankstinės informacijos apie nagrinėjamų duomenų struktūras, gautus rezultatus lyginti sunku. Rekomenduojama objektų klasterizavimui taikyti keletą klasterizavimo metodų.

Paprastai konkretaus analizuojamo daugiamačių duomenų rinkinio parametrų (požymių) reikšmės kinta skirtinguose intervaluose arba jos išreikštos skirtingais matavimo vienetais (pavyzdžiui, kilogramai, metrai, laipsniai). Todėl prieš analizuojant duomenis būtina suvienodinti šių reikšmių mastelius ir tai atliekame naudojant transformaciją, suvedančią duomenis į intervalą nuo nulio iki vieneto:

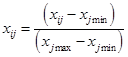.(2.15)

 

2.3 uždavinys.

2.7 lentelė. 2.3 uždavinio duomenys.

Suklasterizuoti naudojant Manheteno atstumą objektų panašumui ir panaudoti centrų principą klasterių jungimui.

Manheteno:

(2.16)

Naudojant Manheteno atstumo matą, sudarome atstumų tarp objektų matricą d_ij:

2.8 lentelė. 2.3 uždavinio atstumų tarp objektų d_ij matrica, naudojant Manheteno atstumo matą.

Mažiausias atstumas tarp 9 ir 4 objekto, todėl juos apjungiame į klasterį. Atstumus tarp klasterių jungiame centrų principu.

(2.17)

2.9 lentelė. 2.3 uždavinio klasterių jungimas centrų principu.

Mažiausias atstumas tarp klasterių 7 ir 1.  Taip pat tarp klasterių 8 ir 7. Pasirenkame apjungti 7 ir 1 į naują klasterį (7,1). Išbraukiame eilutes ir stulpelius su 7 ir 1, o jų vietoje įrašome naują klasterį (7,1).

2.10 lentelė. 2.3 uždavinio klasterių jungimas.

Mažiausias atstumas yra 2,5 . Išbraukiame eilutes ir stulpelius 10 ir (4,9), o jų vietoje įrašome naują klasterį (10,(4,9)).

2.11 lentelė. 2.3 uždavinio klasterių jungimas.

Toliau jungiame 5 ir 3.

2.12 lentelė. 2.3 uždavinio klasterių jungimas.

Šeštą prijungiame prie (7,1) ir perskaičiuojame atstumus.

2.13 lentelė. 2.3 uždavinio klasterių jungimas.

Toliau apjungiame 8 ir 2.

2.14 lentelė. 2.3 uždavinio klasterių jungimas.

2.15 lentelė. 2.3 uždavinio klasterių jungimas.

2.16 lentelė. 2.3 uždavinio klasterių jungimas.

Nubrėžiame dendrogramą.

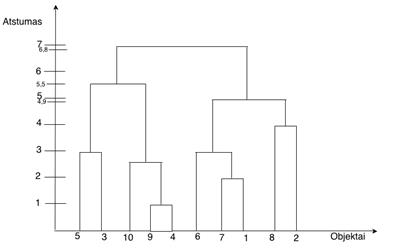
2.7 pav. 2.3 uždavinio dendrograma.

2.4 uždavinys.

Suklasterizuoti objektus ir nubraižyti dendrogramą. Atstumų matricą skaičiuoti panaudojant Manheteno metriką, klasterių jungimui – artimiausių kaimynų.

2.17 lentelė. 2.4 uždavinio duomenys.

Sudarom atstumų matricą:

2.18 lentelė. 2.4 uždavinio atstumų matrica.

Apjungiame 3 ir 4.

2.19 lentelė. 2.4 uždavinio klasterių jungimas.

Apjungiame 1 ir 6.

2.20 lentelė. 2.4 uždavinio klasterių jungimas.

Apjungiame 5 ir 2.

2.21 lentelė. 2.4 uždavinio klasterių jungimas.

Apjungiame (1,6) ir (2,5)

2.22 lentelė. 2.4 uždavinio klasterių jungimas.

Nubrėžiame dendrogramą.

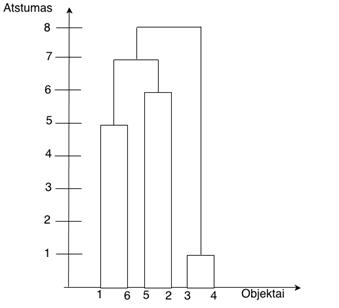
2.8 pav. 2.4 uždavinio dendrograma.

2.5 uždavinys.

Analizuojami duomenys (objektai) - Lietuvos administracinės teritorijos, kurių yra m=60. Duomenys paimti iš http://www.stat.gov.lt (2010 metų). Objektus apibūdinantys parametrai yra n=5:

x₁ – gyventojų skaičius metų pradžioje,

x₂ – tiesioginės užsienio investicijos vienam gyventojui litais,

x₃ – vidutinis mėnesinis darbo užmokestis (neto),

x₄ – gimusių skaičius per metus,

x₅ – gyvulių skaičius namų ūkiuose metų pradžioje.

 

Atsižvelgiant į šiuos penkis parametrus sugrupuosime Lietuvos administracines teritorijas. Iš pradžių, kad suvienodintume požymių mastelius, duomenis transformuosime, suvesdami juos į intervalus nuo 0 iki 1, pagal formulę: 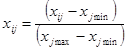. Transformuoti duomenys pateikti 4 priede. Skaičiavimai atliekami R paketu:

 

rduom <- read.table("duom.txt", header=T)

duom <- rduom[,1:5]

rownames(duom) <- rduom[,6]

#sunormuojame duomenis

duom <- (apply(duom, 2, function(x)(x-min(x))/(max(x)-min(x))))

d <- dist(duom, method = "euclidean") # apskaiciuojama atstumu matrica

fit <- hclust(d, method="complete")

plot(fit, xlab="Objektai", ylab="Aukštis", sub="", main="Dendrograma") # atvaizduojame dendograma

groups <- cutree(fit, k=5) # suskaidyti medi i penkis klasterius

# atskiriame raudonai penkis klasterius

rect.hclust(fit, k=5, border="red")

 

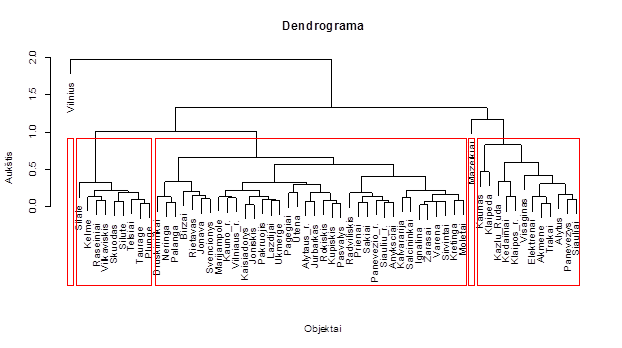
2.9 pav. 2.5 uždavinio dendrograma.

Iš dendrogramos matome, jei atskelsime penkis klasterius, tai du klasteriai bus tokie, kuriuose yra po vieną elementą – miestą, sipriai besiskiriantį nuo kitų. Tai Vilnius ir Mažeikiai.