7.      Riboto endogeninio kintamojo modeliai

7.1.      Binariniai endogeniniai kintamieji

Binariniam endogeniniam kintamajam galioja:

(7.1)

Tiesinis tikimybinis modelis binariniam atvejui:

Funkciją  galima išreikšti kaip tiesinę funkciją, priklausančią nuo X ir parametrų β. Tokiu atveju gauname, kad

(7.2)

Tokiu atveju paklaida randama kaip tikimybė, kad konkretus įvykis įvyks

 ir (7.3)

Pagrindinė problema yra ta, kad tiesinės funkcijos reikšmės  retai kada telpa į intervalą nuo 0 iki 1. Be to modelyje pasireiškia heteroskedastiškumas. Šio modelio pranašumai tie, kad jis paprastas ir tinkamas tuo atveju, kai laisvasis kintamasis yra intervale [0, 1], kitais atvejais modelis nėra labai tikslus ir retai kada taikomas.

Regresinis atvejis:

Regresiniame metode yra du skirtingi atvejai („logit“ ir „probit“), kurie skiriasi tik paklaidų pasiskirstymų, tačiau praktiškai galima teigti, jog yra ekvivalentūs.

Nagrinėjamu atveju, tiriamas modelis atrodys taip:

(7.4)

kur G yra didėjanti tikimybinė funkcija, kuri gali būti:

Logistinė, „logit“ modeliui:

(7.5)

Normalinė, „probit“ modeliui:

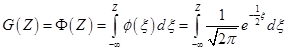(7.6)

Įverčiai randami maksimalaus tikėtinumo metodu.

Tankio funkcija esamuoju atveju atrodytų taip:

, Y_i=0,1;(7.7)

Tada tikėtinumo funkcija bus tokia:

(7.8)

Remiantis maksimalaus tikėtinumo metodu pirmiausiai išlogaritmuojama tikėtinumo funkcija:

(7.9)

Iš gautos išlogaritmuotos funkcijos randami β įverčiai.

Rasti gautų įverčių paklaidas yra sudėtinga, todėl pasinaudojama gautų įverčių β kovariacijų matrica. Ši matrica yra simetrinė, (k+1xk+1) matavimo

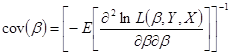(7.10)

Kovariacijų funkcija įtraukia antros eilės dalines išvestines pagal β.

Prognozės rezultatas taip pat yra 1 arba 0. Atliekant prognozę, atsižvelgiama į funkcijos G(X_iβ)  reikšmę. Jei G(X_iβ) <0.5 tada Y_i=0, priešingu atveju, t.y. jei G(X_iβ)>0.5, tada Y_i=1.