8.      Laiko eilučių analizė

8.4.      Laiko eilučių dedamosios

Statistiniai metodai, skirti laiko eilutės elgesio ateityje (arba praeityje) prognozei, iš esmės skiriasi nuo statistinių metodų kurios nors statistinės duomenų imties analizės. Žinant net ypač tikslų laiko eilutės elgesio praeityje aprašymą, nėra jokio teorinio patvirtinimo, kad šis elgesys išliks toks pat ateityje. Vis dėlto tokios prognozės daromos, nes empirinė žmonijos patirtis rodo, kad tai, kas įprasta praeityje, paprastai įvyksta ir ateityje.

Prognozės sėkmė daug priklauso nuo to, ar stebimo kintamojo prigimtis yra stochastinė - atsitiktinė, ar determinuota - apibrėžta. Akivaizdu, kad lengviau prognozuojami determinuoti kintamieji. Tačiau nėra nei visiškai atsitiktinių, nei visiškai determinuotų kintamųjų. Paprastai stebimos abi dedamosios: atsitiktinė ir apibrėžtoji.

Apibrėžtoji dedamoji susideda iš tokių dalių:

·                tiesinio trendo;

·                sezoninių svyravimų;

·                ciklinio svyravimo.

Šios dalys gali būti visos, gali kai kurių (o gal ir visų, jei laiko eilutė griežtai atsitiktinė) nebūti. Paveikslėliuose (8.1-8.4 pav.) pavaizduotos kai kurios situacijos.

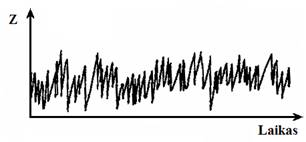
8.1 pav. Vien tik atsitiktinė dedamoji

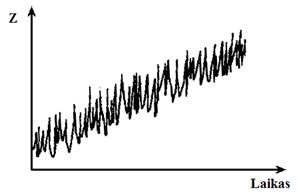
8.2 pav. Tiesinis trendas ir atsitiktinė dedamoji

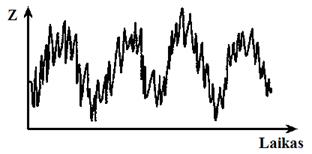
8.3 pav. Sezoniniai svyravimai ir atsitiktinė dedamoji

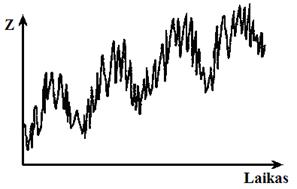
8.4 pav. Tiesinis trendas, sezoniniai svyravimai ir atsitiktinė dedamoji

8.4.1.          Tiesinis trendas

Tiesinis trendas atspindi pagrindines bei ilgalaikes laiko eilutės tendencijas, esminius tiriamo proceso bruožus. Žemės rutulio gyventojų skaičius, nepaisant stichinių nelaimių, karų bei kitų trukdymų, visą laiką didėja. Šis didėjimas nėra visai atsitiktinis - jis gana apibrėžtas. Šiaip trendas gali būti ir netiesinis (pavyzdžiui, logaritminis, eksponentinis ir pan.). Beje, trendo gali ir nebūti (tiksliau, jis gali būti lygus konstantai).

Trendo gali būti ieškoma įvairiais metodais. Dažniausiai tam naudojama regresija. Čia trumpai apibūdinamas vienas iš senesnių trendo išskyrimo metodų - mechaninis išlyginimas, naudojant slenkantį vidurkį. Šio metodo esmė yra ta, kad faktinės laiko eilutės reikšmės pakeičiamos tam tikro eilutės poaibio reikšmių vidurkiais. Procedūros pradžioje parenkamas suglodinimo intervalas - kuo jis ilgesnis, tuo gautasis trendas yra glodesnis, tačiau tada pertvarkytoji eilutė labai sutrumpėja. Šioje vietoje būtinas kompromisas. Be to, parenkant suglodinimo intervalą, paprastai atsižvelgiama į eilutės cikliškumą ar sezoniškumą.

8.4.2.          Sezoniniai svyravimai

Sezoniniai svyravimai - reguliarus stebimo kintamojo reikšmių didėji­mas bei mažėjimas griežtai apibrėžtais laiko periodais. Sezoniniai svyravimai yra identifikuojami lengviausiai iš visų sudėtinių laiko eilutės dedamųjų. Jau iš grafinio duomenų vaizdavimo paprastai galima nustatyti, ar tokie svyravimai egzistuoja, o jeigu taip, koks yra jų periodas. Tuomet kitas uždavinys - įvertinti šiuos svyravimus kiekybiškai, t.y. nustatyti stebimo atsitiktinio dydžio vidurkius, taip pat vidutinius kiekvieno sezono vidurkių indeksus. Paprastai prieš atliekant skaičiavimus, iš laiko eilutės reikšmių yra atmetamas trendas. Tuomet gauti rezultatai iliustruoja sezoninius atsilenkimus nuo trendo. Geriau įvertinti laiko eilutės svyravimo mastą, sąlygojamą sezonų kaitos, naudojamas vidutinis kvadratinis nuokrypis:

(8.31)

kur: K – sezonų skaičius,  - vidutinis k - jo sezono indeksas.

Norint pailiustruoti sezoninių svyravimų analizės eigą, remiamasi duomenimis apie turistų (tūkst. žmonių), apsilankančių viešbutyje per 1985-1989 metus, skaičių. Lentelė pateikta I priede.

Šiame pavyzdyje sezoniškumui išskirti bei jam eliminuoti naudojamas slenkančiojo vidurkio (moving average) metodas. Akivaizdu, kad visas periodas sudarytas iš keturių laiko eilutės reikšmių. Vadinasi, naujoji slenkančiojo vidurkio eilutė turi būti sudaryta iš paeiliui einančių keturių senosios eilutės reikšmių vidurkių. Pavyzdžiui, pirmasis jos narys yra (1,861 + 2,203 + 2,415 + l,908)/4 = 2,097. Analogiškai randami kiti nariai. Nėra vieningos metodologijos, kuriems laiko momentams reikia priskirti naujosios eilutės narius. Cituojmame pavyzdyje elgiamasi šitaip: gautosios reikšmės priskiriamos fiktyviems vidurkiniams periodų laiko momentams (stulpelis B - elgiantis griežtai, šios reikšmės užrašomos tarpuose tarp eilučių; kadangi taip padaryti yra techniškai nepatogu, šios reikšmės vaizduojamos kiek nuleistos), po to dvi gretimos reikšmės vėl suvidurkinamos ir taip gaunami trendo eilutės atitikmenys pradinės laiko eilutės laiko momentams (stulpelis C). Paskutiniame stulpelyje pateikiami slenkančio vidurkio reikšmių indeksai (stulpelio C) atžvilgiu. Pavyzdžiui, 1985 metų III ketvirčiui šis indeksas skaičiuojamas šitaip:

(8.32)

Duomenys bei slenkantis vidurkis pavaizduojami grafiškai (žr. 8.5 pav.)

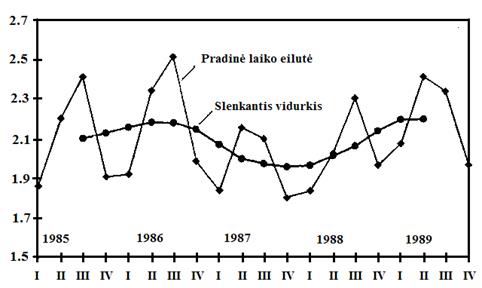
8.5 pav. Pradinės laiko eilutės ir slenkančiojo vidurkio grafikas.

Gautasis slenkantis vidurkis nėra tiesinis trendas - gauta kreivė primena sinusoidę. Čia galima įžvelgti ciklą su trijų metų periodu.

Norint gauti išsamesnes išvadas apie sezoninių svyravimų pobūdį, suskaičiuojami kiekvieno sezono (minėtame pavyzdyje - ketvirčio) vidurkiniai indeksai. Siūloma naudoti vadinamuosius modifikuotus vidurkius, kai atmetami ekstremalūs (pats didžiausias ir pats mažiausias) nariai. Pavyzdžiui, skaičiuojant I ketvirčio vidurkinį indeksą, atmetamos mažiausia (88,6) ir didžiausia (94,5) reikšmės. Tada,

.(8.33)

Analogiškai randami ir kiti vidurkiniai sezonų indeksai:

,(8.34)

,(8.35)

.(8.36)

Indeksų suma . Norėtųsi, kad ji būtų lygi 400 – tuomet vaizdžiau matytųsi sezoniniai nuokrypiai nuo slenkančio vidurkio. Tam tikslui vidurkiniai indeksai normuojami, t. y. padauginami iš konstantos , ir gaunami tokie modifikuoti vidurkiniai ketvirčių indeksai: , ,  ir . Tolimesnė eiga - pagal (8.31) formulę įvertiname laiko eilutės svyravimo mastą:

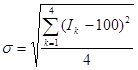 = .(8.37)

Gauti sezoniniai viduriniai indeksai naudojami sudarant naują laiko eilutę, kur eliminuotas sezoniškumas. Kiekvienas pradinės laiko eilutės narys dalijamas iš atitinkamo sezono indekso ir dauginamas iš 100. Pavyzdžiui, pirmasis narys: (l,861/90,3)*100 = 2,061. Iš naujosios eilutės galima gauti trendą, iš kurio eliminuotas sezoniškumo efektas. Remiantis šiuo trendu ir atsižvelgiant į sezoniškumą, galima prognozuoti laiko eilutės ateitį.

8.4.3.          Cikliniai svyravimai

Cikliniai svyravimai yra panašūs į sezoninius, tačiau neturi tokio griežto matematinio aprašymo; jų pasikartojimo periodas nėra toks apibrėžtas, o kalbant apie istorinius procesus - paprastai gerokai ilgesnis. Jeigu sezoninis svyravimas dažnai sutapatinamas su stebimo kintamojo reikšmių svyravimu, susijusiu su metų sezonų ar dar trumpesnių laiko intervalų - savaičių, parų, valandų ir t.t. kaita, tai ciklinis svyravimas istorijoje paprastai apima dešimtmečius, šimtmečius, tūkstantmečius ar dar ilgesnius laikotarpius (pavyzdžiui, valstybių klestėjimas bei žlugimas, visuomeninių ekonominių farmacijų kaita, Žemės ledynmečių pasikartojimas ir pan.).

Ciklinių svyravimų identifikavimas yra gerokai sudėtingesnis negu trendo arba sezoninių svyravimų nustatymas. Tam reikia ilgalaikių duomenų. Be to, juos sukaupus, per stebimą laikotarpį išryškėja vos keletas ciklų, kurių nepakanka patikimoms statistinėms  išvadoms gauti. Dažnai tokiu atveju apsiribojama euristinio pobūdžio samprotavimais, nepagrįstais ma­tematiniu duomenų apdorojimu.

Tuo atveju, kai ciklas identifikuojamas ir sukaupiama pakankamai duomenų jo analizei, naudojami tie patys metodai kaip ir sezoninių svyravimų atveju.