9.      ARFIMA modeliai

9.7.      Praktinis ARFIMA modelio pritaikymas

Remiantis darbe aprašyta teorija ir globalios Žemės temperatūros duomenimis (duomenys paimti iš NASA, adresu (http://data.giss.nasa.gov/), sudarytas modelis, leidžiantis prognozuoti globalinę Žemės temperatūrą. Iš viso 509 stebėjimai. Modelis sudaromas 500 stebėjimų. Paskutinios 9 reikšmės paliktos tam, kad vėliau, atlikus prognozę, būtų galima jas palyginti su prognozuotomis ir apskaičiuoti MSPE.

Modelio sudarymo principus lėmė programinės įrangos galimybės. Modeliavimas buvo atliktas statistinės programos R 2.5, paketo fracdiff pagalba. Jame yra realizuotas ARFIMA modelių parametrų vertinimas. ARFIMA modelis buvo sudarinėjamas remiantis ARIMA modelių identifikavimo, vertinimo ir diagnostinio tikrinimo metodais.

9.7.1.          Duomenų ACF, PACF analizė, GPH testas

ARFIMA modelio pritaikymas laiko eilutės duomenims susideda iš kelių žingsnių: duomenų grafinio atvaizdavimo t atžvilgiu, galimo duomenų transformavimo, priklausomybės eilių nustatymo, parametrų vertinimo bei diagnostinio patikrinimo.

Taigi, žemiau esantis grafikas vaizduoja laiko eilutės duomenis laiko atžvilgiu. Iš grafiko galima matyti, kad duomenys yra nestacionarūs ir turi augantį trendą. Šios laiko eilutės empirinis vidurkis yra 14.00060, o empirinė dispersija - 0.08614761.

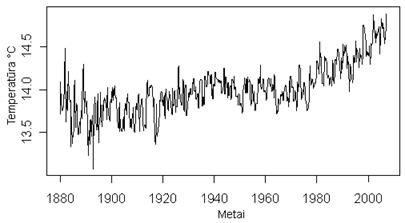
9.1 pav. Globalios žemės temperatūros (ketvirčiais) laiko eilutė

Labai lėtai mažėjančios autokoreliacinės funkcijos reikšmės, didesnės už 0, leidžia įtarti, kad duomenys turi trendą. Be to, lėtas šios funkcijos mažėjimas rodo, jog yra stiprios priklausomybės proceas. Vadinasi, remiantis šia prielaida, galima turimiems duomenims taikyti ARFIMA modelį. Būtent autokoreliacinės funkcijos lėtas eksponentinis gesimas ir byloja apie tai, jog duomenys pasižymi ilga laikine priklausomybe (9.2 pav.).

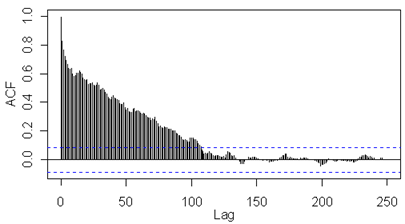
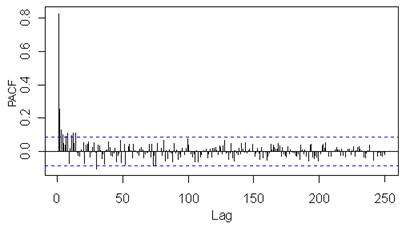
9.2 pav. Autokoreliacinės ir dalinės autokoreliacinės funkcijų grafikai

Dar vienas iš būdų atskleisti ilgos atminties egzistavimą – tai GPH (Gewekw ir Porter-Hudak, 1983) testas. Naudojant šį testą yra įvertinamas trupmeninio diferencijavimo parametras d. Tai yra atliekama statistinės programos R pagalba. Analizuojamiems duomenims įvertintas parametras d yra lygus 0.7796963. Vadinasi, globalios Žemės temperatūros duomenys tikrai yra ilgos laikinės priklausomybės, nestacionarūs (kai d>0 – ilgos atminties: a) nestacionarūs, kai d>0.5 ir b) stacionarūs, kai 0<d<0.5).

9.7.2.          Identifikacijos etapas

Sekantis žingsnis yra p ir q eilių nustatymas bei parametro d įvertinimas. AR(p) ir MA(q) eiles galima nustatyti iš ACF ir PACF grafikų, remiantis 9.1 lentele ir žemiau esančiais ACF ir PACF grafikais (pav. 9.3). Norint lengviau nustatyti, kur autokoreliacinė ir dalinė autokoreliacinė funkcijos gęsta ar nutrūksta, tam tikslui yra sumažinamas lagų skaičius. Kadangi šis vertinimas yra preliminarus, todėl tenka vertinti keletą skirtingų modelių, o vėliau apsispręsti kuris iš modelių yra tinkamiausias. Parenkamas tinkamiausias modelis pagal log tikėtinumo funkciją.

Iš žemiau esančių ACF ir PACF grafikų (pav. 9.4) preliminariai nustatomos p ir q reikšmės. Preliminari autoregresijos polinomo eilė yra 7, o slenkančio vidurkio – 6.

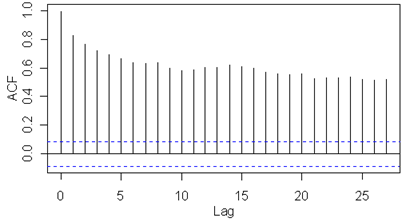
9.3 pav. Autokoreliacinės funkcijos grafikas, kai lagų skaičius

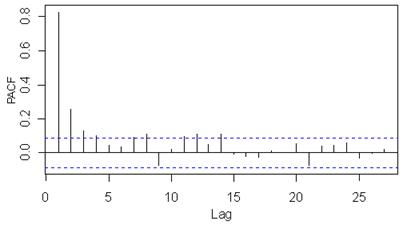
9.4 pav. Dalinės autokoreliacinės funkcijos grafikas, kai lagų skaičius sumažintas

Statistinės programos R dėka galima atlikti AFRIMA modelių parametrų vertinimą. Tam tikslui naudojama funkcija frcdiff: su parametru d kartu įvertinami ir autoregresiniai bei slenkančio vidurkio parametrai.

 

9.2 lentelė. Autoregresijos ir slenkančio vidurkio eilių nustatymas bei d įvertinimas

Preliminarios p ir q eilės iš ACF ir PACF grafikų buvo nustatytos: p=7 ir q=6. Pagal loglikelihood funkciją yra atrenkamas tinkamiausias modelis su p=7, q=7: ARFIMA(7, 0.4244, 7). Antras modelis pagal tinkamumą turimiems duomenims yra ARFIMA(8, 0.3677, 7). Taigi, pasirinkus autoregresijos ir slenkančio vidurkio eiles bei įvertinus parametrus, reikia patikrinti, ar sudarytas modelis yra tinkamas aprašant turimus realius duomenis. Norint atlikti minėtą patikrinimą, reikia tyrinėti paklaidas. Žemiau esantis skyrelis yra skirtas paklaidų analizei.

9.7.3.          Modelio tinkamumo patikrinimas, prognozė

Šiame etape sprendžiama apie modelio tinkamumą, nagrinėjant paklaidas. Šio etapo pirmas žingsnis - grafinis paklaidų arba standartizuotų paklaidų atvaizdavimas laiko atžvilgiu. Jei modelis tinkamas, tai paklaidos turi būti pasiskirsčiusios pagal normalųjį skirstinį su nuliniu vidurkiu ir dispersija, lygia vienam. Jei po modelio parinkimo paklaidos yra dar priklausomos, vadinasi, modelis yra netinkamas duomenims aprašyti.

Jei sukurtas modelis atitinka pradinius duomenis, tada stebimoji liekanų seka yra iš tiesų balto triukšmo realizacija ir jų koreliacinės funkcijos turi tam tikras savybes. Pirmiausia, empirinių ACF ir PACF, paskaičiuotų stebimajai liekanų sekai, reikšmės turėtų tilpti 95 % pasikliautinajame intervale . Šio intervalo rėžiai yra pažymėti liekanų ACF ir PACF grafikuose. Jei daugiau reikšmių nei 5% yra už šio intervalo ribų arba yra keletas labai didelių reikšmių, tai reikia ieškoti duomenims labiau tinkančio modelio.

Diagnostinį patikrinimą galima atlikti Ljung – Box – Pierce statistikos pagalba:

,(9.65)

kur H reikšmė dažniausiai lygi 20. Nulinė hipotezė, jog modelis adekvatus, yra išpildyta, asimptotiškai , kai . Nulinė hipotezė su reikšmingumo lygmeniu α atmetama, jeigu  reikšmė yra didesnė už skirstinio   kvantilį.

Taigi modeliui ARFIMA(7, 0.4244, 7) buvo atliktas diagnostinis patikrinimas (9.5 pav.). Po šio patikrinimo paaiškėjo, jog modelis yra adekvatus.

Tai matosi iš standartizuotų liekanų grafiko, nes tik kelios reikšmės yra didesnės už ±1.96, todėl nėra jokių požymių, kad modelis būtų netinkamas. Priešingu atveju, kai modelis būna netinkamas, tai gerokai daugiau nei 5% liekanų reikšmių yra už šio intervalo ±1.96 ribų ir būna reikšmių, stipriai besiskiriančių nuo visumos.

Taip pat apie modelio tinkamumą galima spręsti pagal gautus paklaidų ACF bei Ljung – Box testo statistikos p reikšmes. Grafikai rodo turimiems duomenims sudaryto modelio adekvatumą. Modelis tinkamas, nes ACF reikšmės neviršija  ribos ir paskutiniame (9.5 pav.) grafike paklaidos tenkina Ljung – Box testo nulinę hipotezę, kuri sako, kad modelis yra adekvatus, jei atitinkamos p reikšmės yra didesnės už pasirinktą reikšmingumo lygmenį (0.05; 0.01; 0.001 ir pan.).

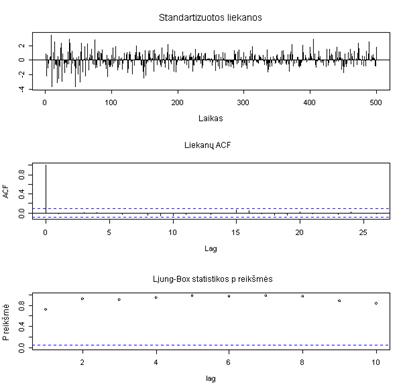
9.5 pav. Modelio ARFIMA(7, 0.4244, 7) diagnostinio patikrinimo grafikas

Po šio patikrinimo paaiškėjo, jog modelis ARFIMA(7, 0.4244, 7) yra adekvatus.

Atlikus diagnostinį patikrinimą, modelis buvo pritaikytas turimiems duomenims ir atlikta prognozė. Žemiau esančioje lentelėje yra pateiktos realių duomenų reikšmės ir prognozuotos su modeliu ARFIMA(7, 0.4244, 7). Šioje lentelėje pateiktos reikšmės nuo 501 iki 509.

9.3 lentelė. Realios ir prognozuotos pagal ARFIMA(7, 0.4244, 7) reikšmės

Atlikus prognozę, taikant modelį ARFIMA(7, 0.4244, 7), yra gauta MSPE=0.021.

Kadangi modelis ARFIMA(8, 0.3677, 7) buvo antras pagal log tikėtinumą (9.2 lentelė), tai šiam modeliui taip pat yra atliekamas Ljung – Box testas, pritaikymas duomenims bei atliekama prognozė devynioms reikšmėms ir apskaičiuojama MSPE, norint parinkti modelį, labiau tinkantį prognozei.

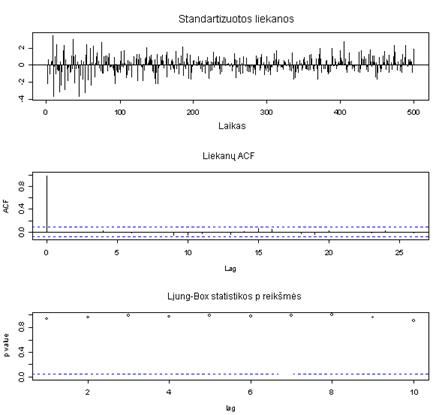
9.6 pav. Modelio ARFIMA(8, 0.3677, 7) diagnostinio patikrinimo grafikas

9.4 lentelė. Realios ir prognozuotos pagal ARFIMA(8, 0.3677, 7) reikšmės

Atlikus prognozę, taikant modelį ARFIMA(8, 0.3677, 7), yra gauta MSPE=0.024.

Modelio ARFIMA(7, 0.4244, 7) vidutinė kvadratinė prognozavimo paklaida yra mažesnė negu modelio ARFIMA(8, 0.3677, 7). Kadangi abiejų modelių MSPE yra labai mažos, tai abu modeliai yra tinkami prognozei. (9.7 pav.) yra pavaizduoti realūs stebėjimai nuo 501 iki 509. (9.8 pav.)– prognozuoti duomenys su modeliu ARFIMA(7, 0.4244, 7). Kadangi atlikta prognozė yra ilgalaikė (prognozavimo ilgis l>6), tai iš pateiktų grafikų yra matyti, kad prognozė yra gana gera.

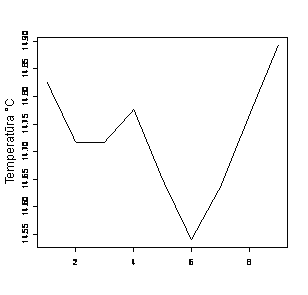
9.7 pav. Realių duomenų grafikas

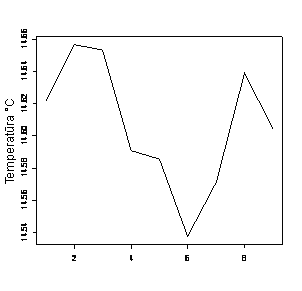
9.8 pav. Prognozuotos reikšmės, naudojant modelį ARFIMA(7, 0.4244, 7)

Norint įvertinti prognozavimo tikslumą, reikia apskaičiuoti vidutinę procentinę absoliutinę paklaidą MAPE:

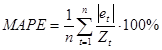.(9.66)

Tikslumą galima nustatyti remiantis 9.5 lentele:

9.5 lentelė. Prognozavimo tikslumo nustatymas

Naudojant prognozei ARFIMA(7, 0.4244, 7) modelį, gauta MAPE yra lygi 0.799%, o su ARFIMA(8, 0.3677, 7) - MAPE=0.875% (skaičiavimų kodas yra pateiktas priede 3). Gautos reikšmės yra labai mažos, todėl prognozavimas yra labai tikslus.