9.      ARFIMA modeliai

9.6.      ARFIMA proceso išraiška ir laiko srities įvertinimas

9.6.1.          Prielaidos ir autoregresinė išraiška

Tarkime, ARFIMA(p, d, q) procesas yra apibrėžiamas:

,(9.38)

kur  yra tiriamo proceso stebėjimų aibė, o  suformuoja naują stacionarią seką, tokią, kurios vidurkis nulinis ir dispersija . Tegul yra polinomai su laipsniais p ir q, tokie, jog , . Tarkime, jog polinomovisos šaknys yra už vienetinio apskritimo ribų taip, jog proceso slenkančio vidurkio dalis yra apgręžiama. Tada galima užrašyti:

.(9.39)

Taip pat laikoma, kad  ir neturi jokių bendrų faktorių, o  šaknys yra už vienetinio apskritimo. Nestacionarumai atsiranda su d reikšmėmis didesnėmis nei .

Išraiška  gali būti išskleista:

,(9.40)

su , , , , . Jei , tai 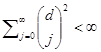 ir (9.40) apibrėžia stacionarų procesą. Su  yra apgręžiamas ir išraiška (9.39) gali būti panaudota, norint gauti begalinės autoregresinės išraiškos  koeficientus ARFIMA proceso :

(9.41)

su , kur .

Trupmeninio diferencijavimo operatorius , kuris formulėje (9.40) yra išskleistas binomine išraiška, gali būti užrašytas kaip . Procesas yra stacionarus, jei p-tos eilės autoregresinio polinomo šaknis  ir q-tos eilės slenkamojo vidurkio dalis,  yra už vienetinio apskritimo ribų, su .

Ilga atmintis dažnai apibūdinama laiko srityje, hiperboliškai mažėjančia autokoreliacijos funkcija, su  arba, dažnių srityje, kur mažiausių dažnių spektras yra  Čia  ir .

ARFIMA proceso prognozei naudojama begalinės autoregresijos išraiška pavidalu  arba

(9.42)

kur  .

Iš praktinės pusės ši forma reikalauja sutvarkymo po h žingsnių (lagų), bet nėra jokio aiškaus būdo kaip tai padaryti.

9.6.2.          Laiko srities įvertinimas

Laiko srities įvertinimus pasiūlė šie autoriai: Hosking (1981), Li ir Mac Leod (1986), Sowell (1992), Tieslau ir kt. (1996). Du paskutinieji buvo aprašę ARFIMA parametrų apjungtą įvertinimą.

Sowell (1992) pateikia tikslų maksimalaus tikėtinumo (ML) algoritmą stacionariems ARFIMA modeliams su išnykstančiomis AR polinomo šaknimis. Kaip minima Baillie (1996), ML yra sudėtingai skaičiuojamas, kadangi kiekvienoje optimizavimo iteracijoje reikia daug skaičiuoti (įskaitant T×T atvirkštinę matricą). Norint gauti įvertinimą, yra naudojami ilgos autoregresijos koeficientų įvertinimai ir ARFIMA(p, d, q) modelio autoregresinis praplėtimas, leidžiantis gauti ilgos atminties parametro d įvertinimą kartu su parametrais, kurie charakterizuoja trumpos atminties modelio dalis.

Prieš apibrėžiant ARFIMA modelio parametrų įvertinimą, pateikiami trys autoregresinės aproksimacijos koeficientų preliminarūs įvertinimai, kuriais paremti ARFIMA modelio įvertinimai. Kiekvienas iš trijų įvertinimų turi tuos pačius apribojimus stacionarumo srityje (kiekvienas priklauso nuo AR eilės parametro p, bet tam, kad supaprastinti skaičiavimo išraišką, ši priklausomybė nebus detaliai aprašyta).

OLS (ordinary least squares) - paprastas mažiausių kvadratų įvertinimas, kuris gali būti naudojamas ir nestacionarioje srityje; dėl šios priežasties OLS taikomas ten, kur stacionarumas normaliai nėra žinomas. Be to, kiti įvertinimo būdai, o būtent Yule-Walker, yra tinkamas norint gauti teorines savybes stacionarumo srityje.

1.      OLS įvertinimas  sprendžia:

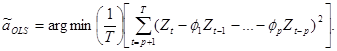(9.43)

2.      Antrasis autoregresinės aproksimacijos koeficientų įvertinimas - spektrinis, kurio asimptotinės savybės buvo ištyrinėtos Yajima (1992) Gauso paklaidoms. Įvertinimo išraiška:

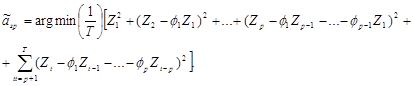(9.44)

3.      Yule-Walker įvertinimas.

Pažymime,  ir , -  matrica su ,  - matrica su elementais 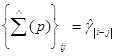. Tada Yule-Walker įvertinimas  sprendžia:

,(9.45)

kur. Nepamirštamas ir (9.45) populiacijos analogas,

(9.46)

kur a(p) sistemos sprendinys.

Visi 3 įvertinimai turi tą patį asimptotinį pasiskirstymą. Todėl naudojamas  žymėjimas kiekvienam iš šių įvertinimų. Yule-Walker įvertinimas naudojamas išvedimuose stacionariu atveju, o nestacionariu atveju yra naudojamas OLS įvertinimas.

Reikšmės a(p) iš (9.46) yra susijusios su stacionaraus ARFIMA proceso begalinės autoregresinės išraiškos koeficientais. Jei būtų pažymėtas begalinės autoregresijos (9.41) koeficientų vektorius , tada jis spręstų:

.(9.47)

Atskiriamas  kaip  ir žymi viršutinę - dešinę matricos dalį, atitinkamai su . Kai

,(9.48)

tai

.(9.49)

Autoregresinis įvertinimas  turės determinuotąjį poslinkį (deterministic bias) išreikštą (9.49).

9.6.3.          Fraktalinio ARMA modelio parametrų vertinimas

Pristačius ARFIMA proceso autoregresinių koeficientų įvertinimus, galima apibrėžti įvertinimus pilnai ARFIMA parametrų aibei, kurie remiasi bet kuriais iš anksčiau aprašytų įvertinimų. Pažymima, jog visų ARFIMA modelio parametrų vektorius yra apskaičiuojamas su , kur , . Tegu  yra bet kuris aukščiau aprašytas autoregresinių koeficientų įvertinimas, ir tegul  žymi vektorių, kuriame yra proceso begalinės autoregresinės išraiškos koeficientai, atvaizduoti kaip  funkcija.

Mažiausio atstumo MD (minimum - distance) įvertinimas su forma,

,(9.50)

yra sukonstruotas panaudojant bet kurį iš  įvertinimų formulėse (9.43-9.45). Begalinės autoregresinės išraiškos koeficientų vektorius yra pateiktas (9.41);  reiškia  svorių matricą.  yra pasirinkta kaip apskaičiuotos  kovariacijų matricos inversija. Tokios svorių matricos panaudojimas suteikia akcentą mažesnių vėlavimų tiksliai nustatytiems koeficientams, kurie duoda apskaičiavimo efektyvumą (jei  tapatumo matrica, tad turima įvertinimo besvorė forma. Naudojant  yra gaunamas svarbus indėlis baigtinės imties tikslumui).

Yra žinoma, jog šis įvertinimas naudoja autoregresinius parametrus vietoje autokoreliacijų, kas leidžia jį naudoti nestacionariems procesams (būtina paminėti, jog ARFIMA(0, d, 0) atveju, įvertinimas gali būti paremtas pirmuoju aproksimuoto AR modelio koeficientu, kadangi pirmasis koeficientas konverguoja į –d šiuo atveju, kuris atitinka (9.40). Tai turi analogiją su šio įvertinimo panaudojimu, Galbraith ir Zinde-Walsh (1994), grynam MA(1) modeliui. Tieslau ir kt. pažymi, kad pastovus d įvertinimas gali būti paremtas pirma autokoreliacija, t.y. .

9.6.4.          ARFIMA modelio parametrų įvertinimas

Atsitiktinio proceso , aprašomo lygtimi (9.6) nežinomų parametrų įverčius galima gauti regresijos metodu. Šis metodas yra pagrįstas spektrinio tankio  išraiška:

,(9.51)

kur

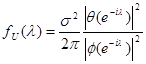(9.52)

yra ARMA(p, q) proceso  spektrinis tankis.

Logaritmuojant (9.51), gaunama

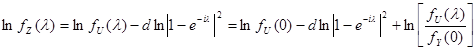.(9.53)

Formulėje (9.53) λ pakeitus į Furjė dažnį  ir prie abiejų pusių pridėjus , kur  yra sekos  periodograma, gaunama:

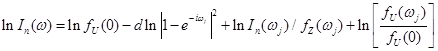(9.54)

Jeigu  yra artimas nuliui, tai paskutiniojo nario įtaka yra nežymi; reiškinys (9.54) gali būti perrašytas paprastos tiesinės regresijos pavidalu:

(9.55)

kur , , , .

Jeigu , seka yra artėtinai tarpusavyje nepriklausomų dydžių seka su  ir tai gali būti panaudota parametro d mažiausių kvadratų įverčiui, kai vertinama  išreikšti per  ir  dėl  tokiu būdu gauname:

.(9.56)

Geweke ir Porter Hudak (1983) parodė, kad egzistuoja tokie m, kad  dėl  ir

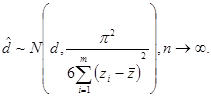(9.57)

Turint d įvertį, lieka įvertinti ARMA(p,q) proceso parametrus . Kadangi, , kur  - ARMA(p,q) procesas, jų Furjė transformacijas pažymėjus atitinkamai , gaunama

.(9.58)

čia  yra paklaidos narys, artėjantis į nulį pagal tikimybę, kai . Pakeitę d į , gauname lygybę:

(9.59)

Pastarajai lygybei pritaikę atvirkštinę Furjė transformaciją, gaunami dydžių  įverčiai:

(9.60)

9.6.5.          ARFIMA modelių sudarymas

ARFIMA (p,d,q) modelių sudarymas susideda iš šių punktų:

1.             duomenų grafinis atvaizdavimas laiko t atžvilgiu;

2.             stacionarumo nustatymas bei galima transformacija;

3.             ACF ir PACF analizė;

4.             preliminarus AR(p) ir MA(q) eilių p ir q nustatymas;

5.             parametrų įvertinimas;

6.             diagnostinis patikrinimas.

 

1.             Duomenų grafinis atvaizdavimas laiko t atžvilgiu – tai pirmasis žingsnis, kurį reikia atlikti analizuojant laiko eilutės duomenis. Iš tokio grafiko galima matyti, ar duomenys turi trendą. Taip pat galima įžvelgti nestacionarumą, kuris yra beveik visose realiose laiko eilutėse.

2.             Stacionarumo nustatymas bei galima transformacija. Duomenų nestacionarumą galima įtarti ir iš autokoreliacinės funkcijos lėto gesimo. Dažniausiai naudojama transformacija:

(9.61)

Transformacija, kuri yra pateikta formule (9.61), nuslopina didelius laiko eilutės reikšmių svyravimus. Kita transformacija – tai Box – Cox laipsninė:

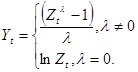(9.62)

Parametras λ pasirenkamas naudojant įvairius metodus. Transformacijos naudojamos normalumo aproksimacijos bei prognozės tiesiškumo pagerinimui.

3.             ACF ir PACF analizė. Iš autokoreliacinės funkcijos ACF ir dalinės autokoreliacinės funkcijos PACF grafikų galima spręsti, koks modelis turimiems duomenims gali tikti.

·                Greitai mažėjanti ACF funkcija reiškia, kad procesas yra silpnos priklausomybės ir jam gali tikti ARMA tipo modeliai.

·                Lėtai mažėjanti ACF funkcija rodo, kad procesas yra stiprios priklausomybės. Labai lėtai mažėjančios ACF teigiamos reikšmės leidžia įtarti, kad duomenys turi trendą.

·                Lėtai gęstanti, svyruojanti ACF rodo sezoninės dedamosios buvimą.

·                Jeigu  visiems , tai gali būti q eilės slenkamojo vidurkio modelis. ACF funkcijos įvertis žymimas .

·                Jeigu  visiems , tai gali būti p eilės autoregresinis modelis. PACF funkcijos įvertis žymimas .

Nagrinėjant minėtas funkcijas, būtina atkreipti dėmesį į horizontalias linijas, rodančias  rėžius, kurie duoda balto triukšmo autokoreliacinės funkcijos artutinį 0.95 lygmens pasikliautinąjį intervalą. Tai reiškia, kad 95% paskaičiuotos  funkcijos taškų turėtų patekti į šį intervalą, jei duomenys yra tarpusavyje nepriklausomų dydžių seka ir balto triukšmo modelis jiems tinka. Jei duomenys tarpusavyje yra priklausomi, tai daugiau nei 5% reikšmių bus už intervalo rėžių.

4.             Preliminarus AR(p) ir MA(q) eilių p ir q nustatymas. Autoregresijos ir slenkančio vidurkio eiles galima nustatyti iš lentelės:

9.1 lentelė. ARMA(p,q) modelių ACF ir PACF elgesys

Jei p=0 ir q>0, ACF nutrūksta po vėlavimo q, o PACF gęsta; jei q=0 ir p>0, PACF nutrūksta po vėlavimo p, o ACF gęsta; jei p>0 ir q>0 tiek ACF, tiek PACF gęsta. Kadangi eilės nustatomos preliminariai, todėl tenka vertinti keletą modelių lygiagrečiai.

5.             Autoregresijos ir slenkančio vidurkio parametrai įvertinami turint fiksuotas p ir q reikšmes, kurios nustatomos naudojant maksimalaus tikėtinumo metodą. Galutinis sprendimas apie modelį turi remtis tikėtiniausiais įverčiais, nes tik šie įverčiai minimizuoja statistiką AICC, kai p ir q yra fiksuoti. Ši statistika apibrėžiama:

(9.63)

kur  - autoregresijos ir slenkančio vidurkio parametrų vektoriai,  - balto triukšmo dispersija ir  - Gauso tipo tikėtinumo funkcija.

6.             Diagnostinis patikrinimas. Jeigu modelis yra gerai parinktas, tada jis turi atspindėti visas tiriamosios sekos savybes ir juo prognozuojant gautos reikšmės turi mažai skirtis nuo tikrųjų. Liekanų sekos tyrimas yra labai svarbus norint įvertinti modelio gerumą. Yra įvairių testų, tiriančių liekanas. Jei sukurtas modelis gerai atitinka duomenis, tai stebimoji liekanų seka yra baltojo triukšmo realizacija. Tokios sekos ACF ir PACF reikšmės turėtų tilpti 95% pasikliautinajame intervale . Jeigu daugiau reikšmių negu 5% yra už šio intervalo ribų arba yra keletas labai didelių reikšmių, tada reikia ieškoti duomenims labiau tinkančio modelio.

Diagnostinį patikrinimą galima atlikti Ljung – Box – Pierce statistikos pagalba:

(9.64)

kur H reikšmė dažniausiai lygi 20. Nulinė hipotezė, jog modelis adekvatus, yra išpildyta asimptotiškai , kai . Nulinę hipotezę su reikšmingumo lygmeniu α atmetame, jeigu  reikšmė yra didesnė už skirstinio   kvantilį.

Modelio pritaikymo paskutinis etapas – tai modelio, kuris bus naudojamas prognozei, parinkimas. Modelis, labiausiai tinkantis prognozei, yra atsirenkamas remiantis vienu iš kriterijų: AIC, AICC, SIC.