2.      Ekonometriniai modeliai

2.2.      Dirbtiniai neuroniniai tinklai (DNT)

DNT – tai informacijos apdorojimo sistemos, paremtos biologinio neurono veikimo principu. Taikomi klasifikavime, prognozavime, optimizavime ir kt. DNT „turi galimybę mokytis“, tai reiškia, kad turint duomenis ir naudojant mokymo algoritmus, tinklas yra priderinamas prie duomenų struktūros taip, kad išmoksta atpažinti naujus duomenis, kurių „dar nematė“.

2.10 pav. Dirbtinio neuroninio tinklo modelis.

DNT modelis turi įėjimus x_k su svoriais w_k, kur k=1,…,n. Paprastai įėjimų ir svorių reikšmės yra realieji skaičiai.

Skaičiuojama pasvertoji suma arba sužadinimo signalas a:

.(2.12)

Neuroną apibūdina aktyvacijos funkcija:

,(2.13)

kurios reikšmė yra:

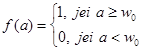- slenkstinė f-ja.(2.14)

čia w₀ – slenksčio reikšmė.

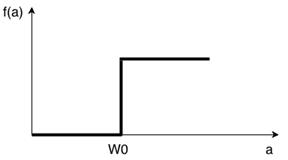
2.11 pav. Slenkstinė funkcija.

Aktyvacijos funkcijos reikšmė – neurono išėjimo reikšmė.

Neuronui apibūdinti naudojamos įvairios aktyvacijos funkcijos, pavyzdžiui, gali būti hiperbolinio tangento:

(2.15)

arba sigmoidinė:

.(2.16)

DNT mokymas – tai jungčių svorių keitimo uždavinys, siekiant, kad tinklas galėtų atlikti jam skirtą užduotį.

Yra trys tinklo mokymo būdai:

1.             Mokymo su mokytoju algoritmai.

2.             Mokymo be mokytojo algoritmai.

3.             Hibridinis mokymas.

 

1) Mokymo su mokytoju algoritmuose vartojama sąvoka „norimos išėjimo reikšmės“. Tai reiškia, kad žinome, pavyzdžiui, kuriai klasei priklauso objektas, arba yra žinoma prognozuojama reikšmė.

Norimos išėjimų reikšmės tiesiogiai susijusios su tinklo išėjimų reikšmėmis. Tinklas koreguojamas keičiant svorių reikšmes. Ieškoma tokių svorių, kad skirtumas tarp norimų išėjimo reikšmių ir reikšmių, gautų išmokius tinklą, būtų kuo mažesnis. (pvz.: perceptrono algoritmas).

2) Čia nėra „norimų išėjimo reikšmių“. Tinklas mokomas ieškoti panašumų (pvz.: saviorganizuojantis neuroninis tinklas (SOM)).

3) Čia dalis tinklo svorių nustatomi pagal mokymą su mokytoju, kita dalis gaunama iš mokymo be mokytojo.

Vienas iš „mokymo su mokytoju“ algoritmų – tai perceptronas. Perceptronas priklauso tiesioginio sklidimo neuroniniams tinklams (galimos tik vienos krypties jungtys iš įėjimų į išėjimus) ir yra sudarytas iš vieno sluoksnio d neuronų su n įėjimų.

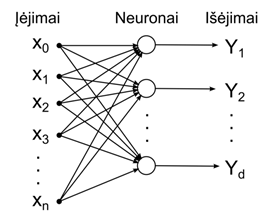
2.12 pav. Tiesioginio sklidimo neuroninis tinklas.

Perceptrono mokymo procese svoriai w_jk keičiami taip, kad pateikus į tinklą vektorių X_i, skirtumas tarp išėjimo vektoriaus Y_i ir norimo vektoriaus T_i būtų kiek galima mažesnis, t.y.

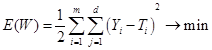,(2.18)

kur  ir , d – išėjimų skaičius, m – įėjimo vektorių skaičius (x-ų rinkinių skaičius), W={w_jk, j=1,...,d, k=0,...,n}. Čia w_jk yra jungties iš k-ojo įėjimo į j-ąjį neuroną svoris.

Funkcija E(W) minimizuojama gradientinio nusileidimo algoritmu, judant antigradiento kryptimi, svorių reikšmes perskaičiuojant kiekvienoje iteracijoje pagal formulę:

(2.19)

Pradžioje w_jk susigeneruojamas, o Δw_jk(t) apskaičiuojamas:

,(2.20)

η yra teigiamas daugiklis, kuris vadinamas mokymo greičiu ir kuriuo reguliuojamas gradientinio optimizavimo žingsnio ilgis, t – iteracijos numeris.

2.2.1.          Perceptrono algoritmas ir jo taikymas ekonometrikoje

Perceptrono algoritmą naudosime norint rasti nežinomus diskriminantinės funkcijos parametrus w_i, i=0,…,l, nustatant sprendimo hiperplokštumą. Paimkime dviejų klasių atvejį kai šios dvi klasės yra atskiriamos tiesiškai. Tai reiškia, jog mes laikome, jog egzistuoja hiperplokštuma, apibrėžta  tokia, kad

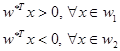.(2.21)

Ši formuluotė taip pat apima ir atvejį, kai , kadangi tai gali būti suvesta į ankstesnę formuluotę, apibrėžiant praplėstą (l+1) dimensijos vektorių . Tada .

Šią problemą galima spręsti kaip paprastą optimizavimo problemą. Tam naudojamas perceptrono algoritmas. Naudojama perceptrono kaina: , kur Y yra mokymo imties vektorių poaibis, kurie yra neteisingai suklasifikuoti hiperplokštumos, apibrėžtos svorių vektoriumi w. Kintamasis , kai  ir , kai .

Akivaizdu, jog J(w) visada yra teigiama ir lygi 0, kai Y neturi sprendinių, t.y. kai visi x suklasifikuojami teisingai. Kai  yra klaidingai suklasifikuojamas, tada  ir  ir jų sandauga duoda teigiamą rezultatą. Tas pats rezultatas gaunamas ir su vektoriais iš klasės w₂. Kai tikslo funkcija pasiekia minimumą – 0, gaunamas sprendimas. Optimizavimui naudojamas gradientinio nusileidimo principas:

(2.22)

kur w(t) yra svorių vektorius nustatytos t-osios iteracijos žingsnyje ir  yra teigiamų realiųjų skaičių seka. Tikslo funkcijos dalinę išvestinę  įstačius į gradientinio nusileidimo išraišką, gauname:

.(2.23)

Šis algoritmas yra žinomas, kaip perceptrono algoritmas ir yra gana paprastos struktūros. Ši funkcija yra apibrėžta visuose taškuose. Algoritmas yra pradedamas atsitiktinai pasirenkant svorių vektorių w(0), o korekcijos vektorius  yra suformuojamas naudojant klaidingai suklasifikuotą informaciją. Svorių vektorius keičiamas atsižvelgiant į sekančią taisyklę. Algoritmu pasiekiamas sprendimas – visi mokymo imties objektai suklasifikuojami teisingai.

Perceptrono algoritmo pseudo kodas:

Atsitiktinai parenkamas w(0)

Pasirenkamas ρ₀

t=0

KARTOTI

Y=Ø

KIEKVIENAM i=1 IKI N

JEI  TAI

PABAIGA

Pakeisti

t=t+1

KOL Y=Ø.

 

2.6 uždavinys.

Turime devynias įmones, kurios tiekia žaliavas. Norime jas suklasifikuoti į patikimas ir nepatikimas. Pirma klasė yra patikimos, o antroji klasė – nepatikimos. Atsižvelgiame į du požymius: X₁ – nuosavų vilkikų, skirtų žaliavų pristatymui, skaičius , o X₂ – garantuojamas žaliavų pristatymo terminas dienomis. Turime patirties su devyniomis įmonėmis. Kai kurios įmonės jau yra sukėlusios problemų dėl žaliavų pristatymo, todėl kai kurias laikome nepatikimomis. Atsižvelgdami į šiuos duomenis, apmokome neuroninį tinklą.

Apmokinę tinklą su šiais duomenimis, norime suklasifikuoti žaliavų tiekėjus į patikimus ir nepatikimus. Pavyzdžiui, į kurią klasę priskirsime tiekėją, jei X₁=2, o X₂=3 ?

2.23 lentelė. 2.6 uždavinio duomenys.

Grafike yra pavaizduoti mokymo imties taškai antros klasės, esantys tiesės kairėje, ir pirmos grupės taškai, esantys tiesės dešinėje.

2.13 pav. 2.6 uždavinio duomenų grafikas.

Ekonominio uždavinio sprendimas atliekamas R statistinio paketo aplinkoje:

 

# sudarome duomenų matricą

duom <- matrix(c(5,1,-1, 7,2,-1, 1,1,1, 1,3,1, 6,5,-1, 3,5,1, 9,5,-1, 9,7,-1, 3,3,1), byrow=T, ncol=3)

# paimame mokymo imtį iš devynių duomenų

mi <- duom[1:9,]

# suformuojame pradinį svorių vektorių

w <- runif(2, -5.0, 5.0)

# pasirenkame pradines reikšmes

ro <- 0.8

t <- 0

# mokymo etapas

repeat {

# pradžioje Y - tuščia aibė

Y <- c()

# tikriname visus mokymo imties narius

for (i in 1:dim(mi)[1]){

# jei suklasifikuotas klaidingai, indeksą dedame į Y

if ((mi[i, 3] * w%*%mi[i,1:2]) >= 0) Y <- c(Y, i)

}

# stspausdiname visus klaidingai suklasifikuotu objektu indeksius

# perskaiciuojame svoriu vektoriu

s <- 0

for (i in Y){

s <- s + (mi[i, 3] * mi[i,1:2])

}

w <- w - ro*s

# pakeiciame kitus parametrus

ro <- ro*0.9

t <- t+1

# jei radome sprendimą - sustabdome

# mokymo imties taškai turi būti atskiriami

if(length(Y) == 0) break()

}

# gauname svorių vektorių

w

# 9.035440 -9.636494

# Apskaičiuojame naujame taške (2;3)

w%*%c(2,3)

# -10.8386

# jei teigiamas - pirma klasė

# patikrinimas

if(w%*%c(2,3)>=0) print("patikimas") else print("nepatikimas")

# "nepatikimas"

 

Atsakymas: tiekėją priskirsimę į nepatikimųjų klasę.