3.      Mažiausių kvadratų metodas (MKM) ir apibendrintas MKM

Praktikoje dažnai funkcinė priklausomybė tarp dviejų dydžių x ir y yra išreiškiama lentele.

3.1 lentelė. Funkcinė priklausomybė tarp dviejų dydžių.

Ekonomikoje, fizikoje, technikoje ir kituose moksluose tokios lentelės – tai eksperimento ar stebėjimo rezultatas. Turėdami tokius duomenis, galime sudaryti analizinę funkcijos išraišką y=f(x,a,b,...). Tokią funkciją vadiname empirine.

Kai tarp x ir y yra tiesinis ryšys, tuomet empirinė funkcija yra tiesinė, t.y.

,(3.1)

kur a ir b yra nežinomi empirinės tiesės parametrai. Šiuos parametrus įvertinti padeda mažiausių kvadratų metodo principas. Nustatant parametrus a ir b reikia reikalauti, kad eksperimento taškai (x_i; y_i) (juodi rutuliukai) būtų kuo arčiau empirinės tiesės. Ši situacija parodyta paveikslėlyje.

3.1 pav. Empirinės tiesės pavizdys, MKM stebėjimų taškai turi būti nutolę nuo tiesės mažiausiu atstumu.

Pažymėkime  Čia taškai  yra empirinėje tiesėje. Skirtumas  vadinamas emprinės funkcijos nuokrypiu. Sudarome tų nuokrypių kvadratų sumą:

(3.2)

Pagal mažiausių kvadratų metodą parametrai a ir b parenkami taip, kad nuokrypių kvadratų suma S būtų minimali. Suma S yra dviejų kintamųjų a ir b funkcija, t.y. S=S(a,b). Vadinasi, turime rasti šios funkcijos minimumą. Tuomet parametrai a ir b turi tenkinti lygčių sistemą

(3.3)

Randame funkcijos S dalines išvestines a ir b atžvilgiu:

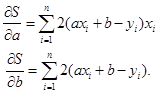(3.4)

Prilyginę išvestines nuliui ir padaliję iš dviejų, gauname:

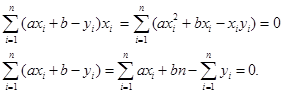(3.5)

Po algebrinių pertvarkymų gauname štai tokią lygčių sistemą:

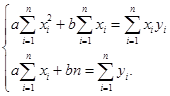(3.6)

Išsprendus sistemą, randamos parametrų reikšmės. Kad taške (a,b) funkcija S įgyja minimumą, išplaukia iš uždavinio esmės, todėl pakankamų ekstremumo sąlygų nenagrinėsime.

3.1 uždavinys.

MKM-u rasti tarp dydžių x ir y tiesinę priklausomybę.

3.2 lentelė. 3.1 uždavinio duomenys.

Pasinaudojus sistema (3.6), gauname:

(3.7)

Išsprendus sistemą, gauname parametrus: a=0,5375 ir b=3,8250, o lygtis tokia: y=0,5375x+3,8250.