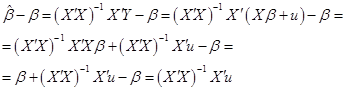3.      Mažiausių kvadratų metodas (MKM) ir apibendrintas MKM

3.2.      Apibendrintas MKM.

Prielaidos klasikinio bendrojo tiesinio regresijos modelio yra:

1.              (Modelis yra tiesinis be trūkstamų kintamųjų ir jame nėra nereikšmingų įtrauktų kintamųjų)

2.              (Paklaidos vektoriaus vidurkis yra nulinis vektorius)

3.              (Vektoriaus u elementai yra homoskedastiški ir nekoreliuoti; n – imties dydis)

4.             X yra  ir „fiksuotas pakartotinėse imtyse“

5.            

Su šiomis prielaidomis paprastas mažiausių kvadratų įvertinys:

(3.14)

yra „geriausias, tiesinis ir nepaslinktas įvertinys“. Tarkime, kad dabar (kai paklaidos koreliuoja):

,(3.15)

kur Ω yra simetrinė, teigiamai apibrėžta matrica su elementais:

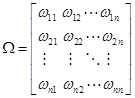(3.16)

kurie pateikia heteroskedastinę paklaidą (Ω matricos pagrindinės diagonalės elementai, kurie yra u elementų dispersijos, gali būti skirtingi) ir yra galima paklaidų lygties autokoreliacija (kovariacija tarp u_i ir u_j yra nelygi nuliui visiems i ≠ j). Aišku, jei ω_ij =0 su visais i ≠ j  ir i,j=1,...,n ir jei ω_ii =1 su i=1,...,n, tai:

(3.17)

ir taip grįžtame į klasikinį modelį.

Kokios yra pasekmės paprasto mažiausių kvadratų (PMK) įvertinio, su sąlyga, jog  PMK įvertinys parametrui β išlieka toks, kaip  ir:

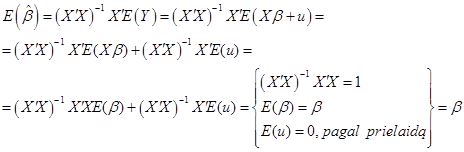(3.18)

Iš to seka, jog  yra nepasliktas įvertinys. Kokios yra PMK įvertinių dispersijos, dispersija  elementų? Dispersijos-kovariacijos matrica  įvertiniui yra apibrėžta kaip:

(3.19)

kur

(3.20)

Įstačius šią išraišką į formulę (3.18) gauname:

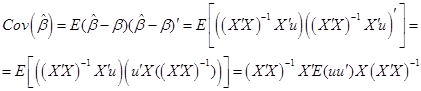                      (3.21)

bet esant prielaidai E(u)=0 formulėje(3.15) turime:

.(3.22)

Iš to seka, kad:

.(3.23)

Prisiminkime, kad klasikiniame modelyje, kur Ω = In, kai , yra dispersijų-kovariacijų matrica, gaunama iš PMK procedūros. Išvada yra tokia, jog jei yra heteroskedastiškumas arba autokoreliacija, arba abu, paklaidos lygtyje, tokioje jog  su Ω ≠ In, tada PMK procedūra pateiks klaidingą dispersijų-kovariacijų matricą parametrui . Vietoje  pateiks  (klaidingą).

Jei Ω žinoma, reikia transformuoti modelį taip, kad būtų tenkinamos visos klasikinės prielaidos. Transformacija yra gaunama per vertinamą lygtį, dauginant iš nestochastinės, nesinguliarios (n×n) matricos P:

(3.24)

tarkime:

,(3.25)

kur PY, X^*=PX ir u^*=Pu ir kur P yra pasirinkta taip, kad:

(3.26)

t.y. , kadangi modelis (3.25) tekina visas klasikinio modelio prielaidas. Taikant PMK metodą transformuotam modeliui (3.25), gauname:

(3.27)

su dispersijų- kovariacijų matrica:

(3.28)

Jei Ω yra žinomas, taikant formulių (3.27) ir (3.28) rezultatus, apibendrintas MKM, yra „geriausias, tiesinis ir nepaslinktas“.