4.      Bendrasis tiesinės regresijos modelis

Bendrasis tiesinis vienos lygties regresinis modelis, atitinkantis d regresorių, aprašomas lygtimi

(4.1)

čia Y – endogeninis kintamasis (dar vadinamas regresantu arba paaiškinamuoju kintamuoju), X₂,…, X_d – egzogeniniai kintamieji (dar vadinami regresoriais, paaiškinančiais kintamaisiais), ε- atsitiktinis faktorius, β₁, β₂,...,β_d – regresijos modelio parametrai. Atitinkamas duomenų Y_t, X_2t, X_3t,…, X_dt, t=1,…,T generavimo mechanizmas aprašomas modeliu

(4.2)

čia ε_t – atsitiktiniai faktoriai, vadinami modelio paklaidomis. Modelį (4.2) galima užrašyti vektoriniu būdu

(4.3)

kai  arba vektoriniu-matriciniu:

(4.4)

kai

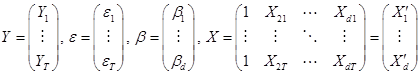.(4.5)

matrica X vadinama plano matrica. Kai turėsime penkių faktorių įtaką, ji bus tokia:

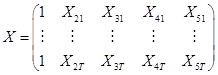.(4.6)

Laikysime, kad, paprastai objektų skaičius T yra didesnis už faktorių skaičių d. Be to, laikysime, kad egzogeninių kintamųjų atžvilgiu yra teisingos šios dvi prielaidos:

A.           Egzogeniniai kintamieji X₂, X_3,…, X_d yra nestochastiniai dydžiai (egzogeniniai kintamieji pastovūs).

B.            Tarp vektorių eilučių (1,…,1), (X₂₁,…, X_2T), ..., (X_d1,…, X_dT) nėra tiesinės priklausomybės (kolinearumo prielaida).

Paklaidoms dažniausiai taikomos sąlygos:

C.            Paklaidos nekoreliuotos, t.y.

(4.7)

D.           Visų padarytų netikslumų vidutinė įtaka kintamajam Y yra nulinė, t.y. Eε₁= ∙∙∙ = Eε_T = 0 (Eε = 0). Tai nulinio vidurkio prielaida.

E.            Homoskedastiškumo prielaida: var(ε_t) = σ² su visais t=1,…,T . Tai reiškia, jog atsitiktinių dydžių ε₁, ...,ε_T skirstiniai turi vienodas dispersijas σ². Paprastai dispersija σ² yra nežinomas neišreikštinis modelio parametras ir aprašo neapibrėžtumų, slypinčių duomenyse, apimtį. Homoskedastinis modelis reiškia, kad kiekviename stebėjime slypinčiai informacijai būdingas vienodas neapibrėžtumas.

 Dažnai sutinkama gausinių paklaidų sąlyga:

F.             Atsitiktiniai dydžiai ε₁, ...,ε_t, t=1,...,T  yra nepriklausomi ir turi vienodą normalinį pasiskirstymą su nuliniu vidurkiu ir dispersija σ².

G.           Liekamoji paklaida yra pasiskirsčiusi nepriklausomai nuo nepriklausomų kintamųjų kitimo:

.(4.8)

Prisiminsime, kad atsitiktinio vektoriaus kovariacinė matrica yra

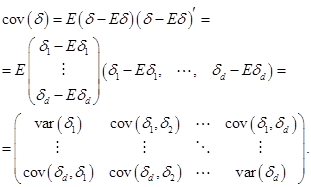(4.9)

Jei paklaidos yra homoskedastinės ir nekoreliuotos, tai

, kur I – vienetinė matrica, kurios dimensija d×d.

Esant teisingoms A, B, C, D, E sąlygoms, modelis (4.2) vadinamas klasikiniu tiesiniu regresiniu modeliu. Kai šiam modeliui teisinga sąlyga F, vadiname gausiniu klasikiniu tiesiniu regresiniu modeliu. Esant teisingai F sąlygai, tada yra teisingos ir C, E sąlygos.