5.      Momentų metodas

Momentų metodas – vienas iš metodų, skirtų gauti parametrų taškiniams įvertiniams. Šis metodas siūlo sulyginti atsitiktinio dydžio momentus su jų empiriniais atitikmenimis ir sudaryti lygčių sistemą:  (ats. dydžio vidurkis = empiriniam vidurkiui, ats. dydžio dispersija = empirinei dispersijai). Lygčių sudaroma tiek, kiek yra nežinomų parametrų. Išsprendus sudarytas lygtis nežinomų parametrų atžvilgiu, gaunami įvertiniai.

Tikimybinį skirstinį, be jo tankio funkcijos, apibūdina jo charakteristikos, vadinamos momentais (dažniausiai naudojami vidurkis ir dispersija). Naudojant momentų metodą, laikoma, kad imties momentų savybės atitinka populiacijos tų pačių momentų savybes. Priklausomai nuo reikiamų įvertinti parametrų skaičiaus yra pasirenkamas atitinkamas momentų skaičius.

Metodo esmę aptarsime vienmatės tiesinės regresijos modelio parametrų įvertiniams rasti. Čia yra du nežinomi parametrai: laisvas narys β₀ ir parametras β₁. Norint juos įvertinti reikia dviejų momentų. Naudosimės vidurkio ir kovariacijos momentais.

Atsižvelgiant į įverčių savybių reikalavimus, vidurkio momento apskaičiavimas remiasi prielaida, kad liekamosios paklaidos e_i vidutinė reikšmė lygi nuliui: E(e_i|x_i)=0 (ankstesniame skyrelyje, prie bendrojo tiesinės regresijos modelio galioja prielaida D, kuri sako, jog Eε=0). Ši išraiška nurodo, kad liekamosios paklaidos vidutinė reikšmė, kai fiksuota nepriklausomo kintamojo reikšmė x_i, yra lygi nuliui. Tai atspindi reikalavimą, kad vidutinės Y reikšmės nebūtų veikiamos sisteminio poveikio, jos „barstosi“ atsitiktinai vidutinės reikšmės atžvilgiu ir vidutinis jų poveikis Y–ui lygus nuliui.

Antrasis šiame metode, naudojamas momentas yra kovariacija, tarp x_i ir e_i, kuri turi būti lygi nuliui (G sąlyga iš ankstesnio skyriaus). Formaliai tai užrašoma taip: cov(e_ix_i)=0.

Ši prielaida nurodo, kad liekamoji paklaida ir nepriklausomas kintamasis tarpusavyje nėra koreliuoti, o priklausomąjį kintamąjį jie veikia atskirai. Jei jų poveikis būtų koreliuotas, ne galima įvertinti kiekvieno jų poveikio Y-ui atskirai. Norint momentų metodu išvesti taškinių įverčių apskaičiavimo formules, reikia prisiminti, kad egzistuoja atitikmenys tarp populiacijos prielaidų ir imties charakteristikų:

Jei E(e)=0, tuomet .

Jei cov(e,x)=0, tuomet .

Nežinomiems įverčiams apskaičiuoti sudaroma lygčių sistema:

(5.1)

Kai vertinami vienmatės tiesinės regresijos modelio parametrai, liekamosios paklaidos įvertis nustatomas taip:

(5.2)

Tuomet lygčių sistemą (5.1) galima užrašyti tokio pavidalo:

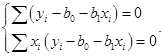(5.3)

Pirmoji šios lygčių sistemos lygtis perrašoma taip:

(5.4)

Čia  ir padalijus šią lygtį iš n, gauname:

(5.5)

Antroji lygčių sistemos lygtis pertvarkoma:

(5.6)

Į paskutinę išraišką įrašome (5.5) ir sutvarkę gauname:

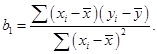(5.7)

Apskaičiuotos b₀ ir b₁ reikšmės yra parametrų β₀ ir β₁ įverčiai.