8. Laiko eilučių analizė
8.1. Sąvokos
Apibrėžimas. Analizuojamo atsitiktinio dydžio ![]() , stebėjimų, gautų laiko momentais
, stebėjimų, gautų laiko momentais
t = 1,...,T eilutė ![]() ,
,![]() ,...,
,...,![]() ,
vadinama laiko eilute.
,
vadinama laiko eilute.
Apibrėžimas. Stacionarios laiko eilutės gali būti
užrašomos autoregresiniais slenkančio vidurkio (ARMA) modeliais. Sakoma, kad
laiko eilutė ![]() ,
, ![]() yra
ARMA(p,q), jei
yra
ARMA(p,q), jei ![]() yra stacionari ir
yra stacionari ir
![]() (8.1)
(8.1)
kur ![]() ,
, ![]() ir
ir ![]() .
Parametrai p ir q (p, q
.
Parametrai p ir q (p, q![]() ) yra vadinami
autoregresijos ir slenkančio vidurkio eilė, o
) yra vadinami
autoregresijos ir slenkančio vidurkio eilė, o ![]() yra
baltasis triukšmas su nuliniu vidurkiu ir dispersija
yra
baltasis triukšmas su nuliniu vidurkiu ir dispersija ![]() .
.
Jei ![]() vidurkis yra nenulinis,
pažymime
vidurkis yra nenulinis,
pažymime ![]() , kur
, kur ![]() , o
tada modelį galime užrašyti:
, o
tada modelį galime užrašyti:
![]() (8.2)
(8.2)
Jeigu ![]() , modelis
(8.1) yra vadinamas p-tos eilės autoregresiniu modeliu AR(p),
kurio pavidalas:
, modelis
(8.1) yra vadinamas p-tos eilės autoregresiniu modeliu AR(p),
kurio pavidalas:
![]() ,(8.3)
,(8.3)
Jei ![]() , modelis
(8.1) vadinamas q-tos eilės slenkančio vidurkio modeliu MA(q),
kurio pavidalas:
, modelis
(8.1) vadinamas q-tos eilės slenkančio vidurkio modeliu MA(q),
kurio pavidalas:
![]() (8.4)
(8.4)
čia ![]() ir
ir ![]() yra konstantos,
yra konstantos, ![]() baltas
triukšmas su nuliniu vidurkiu ir dispersija
baltas
triukšmas su nuliniu vidurkiu ir dispersija ![]() ,
, ![]() ir
ir ![]() .
.
Apibrėžimas. Integruotas ARMA modelis, ARIMA(p,d,q)
yra ARMA modelio plėtinys įtraukiant skirtumų panaudojimą. Sakoma, kad procesas
![]() yra ARIMA(p,d,q), jei
yra ARIMA(p,d,q), jei ![]() yra ARMA(p,q) procesas. Šį modelį galima
užrašyti tokiu būdu:
yra ARMA(p,q) procesas. Šį modelį galima
užrašyti tokiu būdu:
![]() (8.5)
(8.5)
Apibrėžimas. Trupmeniškai diferencijuotas arba
fraktalinis ARIMA(p,d,q), ![]() procesas apibrėžiamas
taip:
procesas apibrėžiamas
taip:
![]() (8.6)
(8.6)
čia ![]() ir
ir ![]() , operatoriai, kurie buvo apibrėžti
anksčiau. Toks modelis yra vadinamas ARFIMA modeliu.
, operatoriai, kurie buvo apibrėžti
anksčiau. Toks modelis yra vadinamas ARFIMA modeliu.
Apibrėžimas. Vektorinis autoregresinis trupmeniškai integruotas slenkančio vidurkio modelis VARFIMA (p,d,q) formaliai gali būti užrašytas:
![]() ,(8.7)
,(8.7)
kur ![]() yra
yra ![]() vektorinis procesas,
vektorinis procesas, ![]() yra
yra ![]() trupmeninio
diferencijavimo operatorius su
trupmeninio
diferencijavimo operatorius su ![]() . Toliau darbe dydis
. Toliau darbe dydis ![]() bus žymimas a(B).
bus žymimas a(B). ![]() - normalūs, vienodai pasiskirstę ir nepriklausomi
atsitiktiniai dydžiai.
- normalūs, vienodai pasiskirstę ir nepriklausomi
atsitiktiniai dydžiai. ![]() yra
yra ![]() dispersijų
- kovariacijų matrica,
dispersijų
- kovariacijų matrica, ![]() , kur
, kur ![]() yra
yra ![]() autoregresinių
parametrų matrica ir
autoregresinių
parametrų matrica ir ![]() , o
, o ![]() yra
yra ![]() slenkančio vidurkio parametrų matrica; B
yra lago (vėlavimo) operatorius.
slenkančio vidurkio parametrų matrica; B
yra lago (vėlavimo) operatorius.
![]() vadinamas VARFIMA (p,
vadinamas VARFIMA (p,![]() ,q) procesu, kur p yra
autoregresinio komponento maksimali eilė, o q - slenkančio vidurkio
maksimali eilė.
,q) procesu, kur p yra
autoregresinio komponento maksimali eilė, o q - slenkančio vidurkio
maksimali eilė.
Vienmatis atvejis, kai ![]() yra
žinomas kaip ARIMA(p,d,q) procesas.
yra
žinomas kaip ARIMA(p,d,q) procesas.
Apibrėžimas. Laiko eilutė ![]() yra
vadinama griežtai stacionaria, jei eilutės
yra
vadinama griežtai stacionaria, jei eilutės ![]() ,
, ![]() , ,...,
, ,...,![]() tikimybinis
elgesys yra toks pat, kaip ir eilutės
tikimybinis
elgesys yra toks pat, kaip ir eilutės ![]() ,
, ![]() , ...,
, ...,![]() elgesys,
bet kuriems laiko momentams
elgesys,
bet kuriems laiko momentams ![]() t
t![]() , t
, t![]() ,...,
,...,![]() bet kokiam skaičiui n = 1,2,...
ir bet kokiam poslinkiui h = 0,
bet kokiam skaičiui n = 1,2,...
ir bet kokiam poslinkiui h = 0,![]() 1,
1,![]() 2,...
2,...
Silpno stacionarumo sąlygos keliamos tik dviem pirmiesiems laiko eilutės momentams, t.y. laiko eilutės vidurkis yra konstanta ir nepriklauso nuo laiko t:
E(![]() ) =
) = ![]() ir kovariacinė funkcija
ir kovariacinė funkcija ![]() (s, t) priklauso tik nuo skirtumo
(s, t) priklauso tik nuo skirtumo
![]() :
:
![]() = E
= E![]() visiems
laiko momentams t, arba
visiems
laiko momentams t, arba ![]() = E
= E![]() .
.
Stacionarių laiko eilučių autokoreliacinė funkcija apibrėžiama taip:
![]() (8.8)
(8.8)
Autokovariacinė funkcija:
![]() cov(
cov(![]() ).(8.9)
).(8.9)
Dalinė autokoreliacinė funkcija:
![]() (8.10)
(8.10)
Apibrėžimas. ARMA(p,q) proceso stacionarumas. ARMA(p,q)
modelis ![]() yra vadinamas stacionariu, jei laiko
eilutė
yra vadinamas stacionariu, jei laiko
eilutė ![]() ,
, ![]() gali
būti užrašyta kaip tiesinis procesas:
gali
būti užrašyta kaip tiesinis procesas:
![]() (8.11)
(8.11)
kur ![]() ir
ir ![]() .
.
ARMA(p,q) procesas yra stacionarus tik tada, kai AR polinomo
![]() (8.12)
(8.12)
šaknys yra už vienetinio apskritimo ribų, t.y. ![]() tik tada, kai
tik tada, kai ![]() .
Tiesinio proceso (8.11) koeficientai gali
būti nustatomi sprendžiant:
.
Tiesinio proceso (8.11) koeficientai gali
būti nustatomi sprendžiant:
![]() .(8.13)
.(8.13)
Apibrėžimas. ARMA(p,q) proceso
apgręžiamumas. ARMA(p,q) modelis ![]() vadinamas
apgręžiamu, jei laiko eilutė
vadinamas
apgręžiamu, jei laiko eilutė ![]() ,
, ![]() gali būti užrašyta kaip
gali būti užrašyta kaip
![]() (8.14)
(8.14)
ARMA(p,q) modelis yra apgręžiamas tik tada, kai MA polinimo
![]() (8.15)
(8.15)
šaknys yra už vienetinio apskritimo ribų.
Koeficientai ![]() išraiškoje (8.14)
gali būti randami sprendžiant:
išraiškoje (8.14)
gali būti randami sprendžiant:
![]() .(8.16)
.(8.16)
Sezoninis autoregresinis slenkančio vidurkio modelis žymimas ARMA(P,Q) užrašomas operatorine forma:
![]() (8.17)
(8.17)
kur operatoriai
![]() ir
ir
![]() .(8.18)
.(8.18)
Operatorinis sezoninis autoregresinis slenkančio vidurkio
modelis, pasiūlytas Box ir Jenkins (1974), žymimas ![]() ,
jis užrašomas tokia forma:
,
jis užrašomas tokia forma:
![]() (8.19)
(8.19)
Operatorinis sezoninis autoregresinis integruotas
slenkančio vidurkio modelis, pasiūlytas Box ir Jenkins (1974), žymimas ![]() , bendras jo pavidalas yra:
, bendras jo pavidalas yra:
![]() (8.20)
(8.20)
kur ![]() .
.
Plačiau apie šiuos ir kitus laiko eilučių modelius galima rasti.
Poslinkio atgal operatorius B:
 (8.21)
(8.21)
Skirtumo operatorius (1-B):
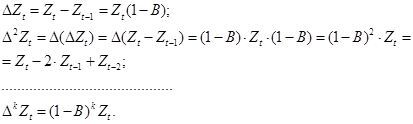 (8.22)
(8.22)
Taigi, ![]() Dydis k pakeičiamas
į d, o
Dydis k pakeičiamas
į d, o ![]() - į
- į ![]() ir
užrašomas tokia forma:
ir
užrašomas tokia forma:
![]() (8.23)
(8.23)
![]() vadinamas trupmeninio
diferencijavimo operatoriumi arba d eilės integruojančiu filtru. Toliau
darbe jis bus žymimas
vadinamas trupmeninio
diferencijavimo operatoriumi arba d eilės integruojančiu filtru. Toliau
darbe jis bus žymimas ![]() .
.




