9.      ARFIMA modeliai

9.3.      Trupmeniškai diferencijuotų laiko eilučių savybės

Tarkime, eilutė  su spektru

(9.14)

kur  - teigiama konstanta. Tai yra eilutė, kuri, diferencijuota d kartų, duoda baltąjį triukšmą. Trupmeninis diferencijavimas reikalingas atveju, kai -1<d<1, bet d≠0. Galima daryti prielaidą, kad  yra gaunamas iš linijinio filtro, pritaikyto nulinio vidurkio baltajam triukšmui ir, kad  turi nulinį vidurkį. Autokovariacijos, jei jos  bus gaunamos iš

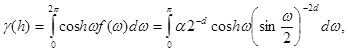(9.15)

atsižvelgiant, kad .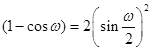

Naudojant standartinę formulę

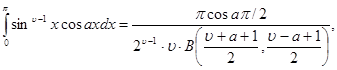(9.16)

tam tikri skaičiavimai duoda:

 su sąlyga, kad -1<d< ir d.

Jei d, tai , skirtumas, yra begalinis. Iš čia seka, kad autokoreliacijos yra gaunamos iš:

(9.17)

kur - Eulerio integralas pavidalu 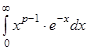,  priklausantis nuo parametro p (p - tikras teigiamas skaičius). Šis integralas, priklausantis nuo parametro p, yra vadinamas gama funkcija ir žymimas t. y.

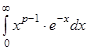, kur gama funkcija pasižymi savybe .

Naudojant standartinę aproksimaciją, gautą iš Sheppard‘o formulės, dideliems j,  yra gerai aproksimuota su , iš čia seka:

(9.18)

dideliems h , ir , d≠0.

Stacionariam ARMA modeliui , o  dideliems h; šios reikšmės eksponentiškai artėja prie nulio ir yra gautos iš (9.18).

Tai iliustruoja ilgos atminties aspektą eilučių su spektru (9.12) arba (9.14).

Begalinio slenkančio vidurkio  pavidalas bus išreikštas iš

(9.19)

naudojant postūmio atgal operatorių B. Iš čia seka, kad  spektras yra:

(9.20)

kur  ir . Taip pat, kai

, nes galima paimti  ir

Toks filtras gali būti pavadintas d eilės integruojančiu filtru. Naudojant standartinį binominį skleidinį:

,(9.21)

seka, kad

, (9.22)

(9.23)

dideliems j ir atitinkamoms konstantoms A.

Tarkime, dabar MA(∞) modelis su   gautas tiksliai iš (9.23), t. y.

(9.24)

toks, kad  Ši eilutė turi dispersiją.

Iš begalinių eilučių teorijos yra žinoma, kad

 konverguoja su s>1,

o priešingu atveju diverguoja. Taip pat yra lengvai parodyta, kad  dispersija skiriasi nuo  tik baigtiniu dydžiu, iš čia seka, kad  dispersija yra baigtinė kai gauta su d<, ir begalinė jei d.

AR(∞) pavidalas yra:

      (9.25)

t. y. , arba ,

kuris duoda spektrą:

(9.26)

tokį, kurį palyginus su (9.14):

,  (9.27)

ir dideliems j

.(9.28)

Iš (9.23) ir (9.28) matoma, jog  ir  artėja prie 0 lėčiau, nei eksponentiškai. Iš čia seka, kad joks ARMA(p,q) modelis su baigtiniais  p ir q duos pakankamą aproksimaciją dideliems j. Iš (9.22) ir (9.27) galime pažymėti, kad  ir , jeigu  ir , , jeigu .

Atvejis, kai yra tiesiog baltojo triukšmo atvejis , toks, kad  visi yra lygūs nuliui, kai .

Filtras su forma:

,(9.29)

naudojant anksčiau pristatytą frazę, yra d eilės integruojantis filtras ir gali būti pavadintas trupmeninio diferencijavimo operatoriumi. Tai lengvai matoma paėmus , du kartus pritaikant atitinka eilinį, pilną skirtumą ir pritaikius jį kartą duoda pusę arba trupmeninį, skirtumą.

Šiuo metu dar nėra aišku ar integruoti modeliai su nesveikuoju d  atsiranda praktikoje ir tik išplėstiniai empiriniai tyrinėjimai gali išaiškinti šią situaciją. Kai kurie rezultatai aprašyti Granger (1980) daro išvadą, jog šie modeliai gali būti svarbūs realiems ekonominiams kintamiesiems.