9. ARFIMA modeliai
9.4. Metodai, kurie atskleidžia ilgos atminties egzistavimą
Beran 1994 m. yra aprašęs metodus, kurie nustato ilgos atminties egzistavimą. Šiam tikslui yra naudojami grafiniai metodai, parametriniai (Whittle MT metodas) ir pusiau parametriniai metodai (GPH metodas ir lokalus Whittle metodas). Ilgos atminties parametrinių modelių parametriniai metodai įvertina d parametrą per maksimalaus tikėtinumo įvertinimą. Minėti metodai pateikia tikslesnį d įvertinimą negu kiti metodai. Pusiau parametriniai metodai, tokie kaip GPH (Geweke ir Porter Hudak, 1983), siekia įvertinti d pagal kelias ankstesnes laiko eilutės spektrinio tankio prielaidas ir be tiksliai nusakyto baigtinių parametrų modelio. GPH testas naudojamas patikrinti nulinei hipotezei ilgos atminties egzistavimo. Maksimalaus tikėtinumo metodas naudojamas įvertinti trupmeninio diferencijavimo parametrą d.
9.4.1. GPH testas
Geweke ir Porter Hudak (1983) pasiūlė pusiau parametrinį ilgos
atminties ištyrimo būdą. Tam tikras, trupmeniškai integruotas procesas ![]() , kurio spektrinis tankis yra:
, kurio spektrinis tankis yra:
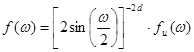 (9.30)
(9.30)
kur ![]() - Fourier dažnis,
- Fourier dažnis, ![]() - spektrinis tankis
- spektrinis tankis ![]() , o
, o ![]() -
stacionarus trumpos atminties trikdymas su nuliniu vidurkiu. Harmoninių dažnių
aibė žymima
-
stacionarus trumpos atminties trikdymas su nuliniu vidurkiu. Harmoninių dažnių
aibė žymima ![]() ir yra lygi:
ir yra lygi:
![]() (9.31)
(9.31)
kur n – imties didumas. Spektriniam tankiui ![]() pritaikius logaritmavimą, gaunama
formulė:
pritaikius logaritmavimą, gaunama
formulė:
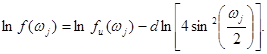 (9.32)
(9.32)
Aukščiau esančią formulę (9.32) galima užrašyti alternatyvia forma:
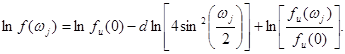 (9.33)
(9.33)
Trupmeninio skirtumo parametras d gali būti apskaičiuotas iš regresinių lygčių, sudarytų iš formulės (9.33).
Geweke ir Porter Hudak (1983) parodė, kad naudojimas
periodogramos įverčio ![]() , jeigu dažnių
, jeigu dažnių ![]() skaičius panaudotas regresijos formulėje (9.33)
yra imties didumo n funkcija
skaičius panaudotas regresijos formulėje (9.33)
yra imties didumo n funkcija ![]() , kur
, kur ![]() ir
ir ![]() -
teigiamas sveikasis skaičius, tai mažiausių kvadratų įvertinimas
-
teigiamas sveikasis skaičius, tai mažiausių kvadratų įvertinimas ![]() , naudojant aukščiau minėtą regresiją,
yra asimptotiškai normaliai pasiskirstęs didelėje imtyje:
, naudojant aukščiau minėtą regresiją,
yra asimptotiškai normaliai pasiskirstęs didelėje imtyje:
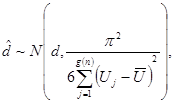 (9.34)
(9.34)
kur 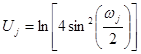 ir
ir ![]() - tai imties vidurkis
- tai imties vidurkis ![]() ,
, ![]() . Su nuline
hipoteze, jog nėra ilgos atminties (d=0), t statistika turi
ribinį standartinį normalųjį pasiskirstymą:
. Su nuline
hipoteze, jog nėra ilgos atminties (d=0), t statistika turi
ribinį standartinį normalųjį pasiskirstymą:
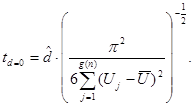 (9.35)
(9.35)




